Определение.Уравнения, в которые неизвестная функция входит под знаком производной или дифференциала, называются дифференциальными уравнениями

Подобными уравнениями описываются многие физические явления и процессы.

Дифференциальное уравнение - мощное средство математического моделирования процессов окружающей нас действительности, широкое использование которых обусловлено как относительной простотой установления дифференциальных связей между исследуемыми величинами (в основном благодаря линеаризации этих связей), так и универсальность их применения

Примеры.

1) 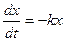- уравнение радиоактивного распада (k – постоянная распада, х – количество неразложившегося вещества в момент времени t, скорость распада пропорциональна количеству распадающегося вещества).

2) 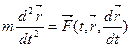- уравнение движения точки массы т под влиянием силы F, зависящей от времени, положения точки, определяемого радиус-вектором r, и ее скорости 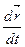. Сила равна произведению массы на ускорение.

3) - уравнение Пуассона, задающее зависимость между многими физическими величинами. Например, можно считать, что u(x,y,z) – потенциал электростатического поля, а ρ(x,y,z) – плотность зарядов.

Мы будем рассматривать уравнения, где неизвестная функция является функцией одной переменной. Такие уравнения называются обыкновенными дифференциальными уравнениями.

Определение Уравнение вида

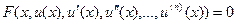(29.1)

называется обыкновенным дифференциальным уравнением п -го порядка. При этом порядком уравнения называется максимальный порядок входящей в него производной.

Если независимая переменная одна, то уравнение называется обыкновенным, если же независмых переменных две или больше, то уравнение называется уравнением в частных производных.

Определение Функция, которая при подстановке в уравнение (29.1) обращает его в тождество, называется решением дифференциального уравнения.

Процесс нахождения решения дифференциального уравнения называется интегрированием дифференциального уравнения.

Дифференциальным уравнением первого порядка называется уравнения вида .

Если это уравнение можно решить относительно у', то его можно записать в виде

(29.2).

Определение Общим решением дифференциального уравнения первого порядка в области D называется функция , обладающая следующими свойствами:

1) она является решением данного уравнения при любых значениях произвольной постоянной С, принадлежащих некоторому множеству;

2) для любого начального условия 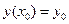такого, что , существует единственное значение 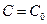, при котором решение 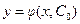удовлетворяет заданному начальному условию.

Всякое решение 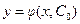, получающееся из общего решения при конкретном значении 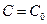, называется частным решением.

Задача, в которой требуется найти частное решение уравнения , удовлетворяющее начальному условию 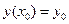, называется задачей Коши.

Построенный на плоскости хОу график всякого решения дифференциального уравнения называется интегральной кривой этого уравнения.

Таким образом, общему решению на плоскости хОу соответствует семейство интегральных кривых, зависящее от одного параметра - произвольной постоянной С, а частному решению, удовлетворяющему начальному условию 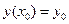, - кривая этого семейства, проходящая через заданную точку.

Геометрический смысл уравнения

Пусть дано дифференциальное уравнение первого порядка у' = f (x, у) и пусть функция - его решение. График решения представляет собой непрерывную интегральную кривую, через каждую точку которой можно провести касательную. Из уравнения следует, что угловой коэффициент у' касательной к интегральной кривой в каждой ее точке (х; у) равен значению в этой точке правой части уравнения f (х, у). Таким образом, уравнение у' = f (x, у) устанавливает зависимость между координатами точки (х; у) и угловым коэффициентом у' касательной к графику интегральной кривой в той же точке. Зная х и у, можно указать направление касательной к этой интегральной кривой в точке (х; у).

Сопоставим каждой точке (х; у) интегральной кривой направленный отрезок, угловой коэффициент которого равен f (x, у). Получим так называемое поле направлений данного уравнения, раскрывающее геометрический смысл дифференциального уравнения первого порядка.

Итак, с геометрической точки зрения уравнение у' = f (x, у) определяет на плоскости Оху поле направлений, а решение этого уравнения - интегральная кривая, направление касательной к которой в каждой точке совпадает с направлением поля в этой точке.

Построив на плоскости поле направлений данного дифференциального уравнения, можно приближенно построить интегральные кривые.

Примеры.

1) 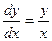. В каждой точке, кроме начала координат, угловой коэффициент к искомой интегральной кривой равен , то есть тангенсу угла, образованного с осью О х прямой, проходящей через данную точку и начало координат. Следовательно, интегральными кривыми в данном случае будут прямые вида у = сх (рис.1).

у

у

х

х

Рис. 1. Рис. 2.

2) 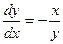. В этом случае касательная в каждой точке плоскости перпендикулярна направлению прямой, проходящей через эту точку и начало координат, так как угловые коэффициенты этих прямых удовлетворяют условию ортогональности: 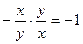. Поэтому направление касательной в данной точке совпадает с направлением касательной к окружности с центром в начале координат, на которой лежит выбранная точка. Такие окружности и являются интегральными кривыми данного уравнения (рис. 2).

Часто для построения интегральных кривых удобно предварительно найти геометрическое место точек, в которых касательные к искомым интегральным кривым сохраняют постоянное направление. Такие линии называются изоклинами.

Пример.

Изоклины уравнения задаются уравнениям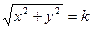и или 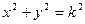, так как на каждой изоклине производная должна сохранять постоянное значение. Полученные уравнения задают семейство концентрических окружностей с центром в начале координат, а угловой коэффициент касательной к интегральной кривой равен радиусу проходящей через данную точку окружности.

Задача Коши для уравнения первого порядка

Как уже было сказано, общим решением уравнения (29.2) является все множество функций, обращающих при подстановке рассматриваемое уравнение в тождество. Пусть теперь требуется найти решение этого уравнения, удовлетворяющее условию

у (х₀) = у₀, (29.3)

называемому начальным условием. Если общее решение уравнения (29.2) задается формулой

у = φ (х, С), (29.4)

то значение постоянной С, соответствующее поставленному начальному условию, можно определить, подставив в равенство (29.4) х = х₀ и у = у₀.

Определение Задача выбора из общего решения (29.4) уравнения (29.2) решения, удовлетворяющего начальному условию (29.3), называется задачей Коши, а выбранное решение называется частным решением уравнения (29.2).

Замечание. Если воспринимать множество всех решений уравнения (29.2) как множество интегральных кривых на плоскости, то ставится задача поиска той из них, которая проходит через точку с координатами (х₀, у₀).

Выясним, при каких условиях такая кривая существует и является единственной.

Теорема существования и единственности задачи Коши

Теорема Коши. Если функция f(x,y) непрерывна и имеет непрерывную производную у' в области D, то решение дифференциального уравнения при начальном условии 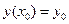существует и единственно, т.е. через точку проходит единственная интегральная кривая данного уравнения.

Особым решением называется такое решение, во всех точках которого; условие единственности не выполняется, т. е. в любой окрестности каждой точки (х; у) особого решения существуют по крайней мере две интегральные кривые, проходящие через эту точку.

Особые решения не получаются из общего решения дифференциального управления ни при каких значениях произвольной постоянной С (в том числе и при С= ± ).

Особым решением является огибающая семейства интегральных кривых (если она существует), т. е. линия, которая в каждой своей точке касается по меньшей мере одной интегральной кривой.

Например, общее решение уравнения 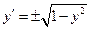записывается в виде . Это семейство интегральных кривых имеет две огибающие: у=1 и у =-1, которые и будут особыми решениями.

Методы решения простейших дифференциальных уравнений первого порядка.

1. Уравнения с разделяющимися переменными.

Дифференциальные уравнения вида

f₂(y)dy = f₁(x)dx (30.1)

называются уравнениями с разделяющимися переменными.

Тогда любое решение у(х) этого уравнения будет удовлетворять и уравнению

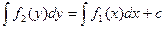, (30.2)

где с – произвольная постоянная. Если удается найти первообразные функций f₁(x) и f₂(y), выраженные в элементарных функциях, то из (38.2) можно получить конечное уравнение вида

Ф (х, у) = 0, (30.3)

которое определяет решение уравнения (30.1) как неявную функцию х.

Определение Уравнение вида (30.3) называется интегралом уравнения (30.1), а если оно определяет все решения (30.1) – общим интегралом этого уравнения.

Пример.

. Приведем уравнение к виду (30.1): 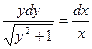, откуда 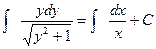. Проинтегрируем обе части равенства: 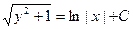. Полученное уравнение можно считать общим интегралом или решением исходного уравнения.

Если требуется найти частное решение уравнения (30.1), удовлетворяющее условию у(х₀)=у₀, достаточно подставить значения х₀ и у₀ в уравнение (30.3) и найти значение с, соответствующее начальному условию.

Пример.

Найти решение уравнения y′ ctg x + y = 2, удовлетворяющее условию у (0) = -1.

Разделим переменные: 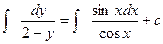, -ln | 2 – y | = -ln | cos x | - ln | c |,

2 – y = c • cos x. Подставив в это равенство х = 0 и у = -1, получим, что с = 3. Следовательно, искомое частное решение имеет вид: y = 2 – 3cos x.

2. Уравнения, приводимые к уравнениям с разделяющимися переменными.

Если требуется решить уравнение вида

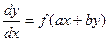, (30.4)

где а и b – постоянные числа, то с помощью замены переменной z = ax+by оно сводится к уравнению с разделяющимися переменными:

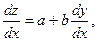
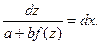
Пример.

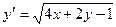. Замена: z = 4 x + 2 y – 1, тогда + с. Вычислим интеграл в левой части равенства: замена 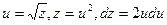приводит к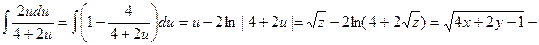

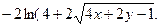Проинтегрировав теперь правую часть равенства, получим общий интеграл:

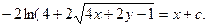
Дата добавления: 2014-01-04