Однородные линейные дифференциальные уравнения с постоянными коэффициентами. Построение фундаментальной системы решений

План.

1. Однородные линейные дифференциальные уравнения с постоянными коэффициентами. Построение фундаментальной системы решений.

2. Неоднородные линейные дифференциальные уравнения. Частное и общее решения.

3. Методы нахождения частного решения неоднородного линейного дифференциального уравнения.

Определим вид частных решений однородного линейного уравнения

, (34.8)

в котором коэффициенты a_i постоянны. Можно показать, что они имеют вид , где k – постоянная. Действительно, при этом , и после подстановки в уравнение (34.8) получаем:

,

или, после сокращения на e^kx,

- (34.9)

так называемое характеристическое уравнение для уравнения (34.8). Числа k, являющиеся его решениями, при подстановке в функцию дают частные решения уравнения (34.8). Исследуем различные возможности количества и вида решений характеристического уравнения.

1. Все корни уравнения (34.9) действительны и различны: k₁, k₂,…, k_n. Тогда они задают максимально возможное количество линейно независимых решений уравнения (34.8) (их линейная независимость показана выше), то есть определяют фундаментальную систему решений. Следовательно, в этом случае общее решение уравнения (34.8) может быть записано в виде:

.

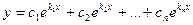Пример.

Общее решение уравнения можно найти, решив характеристическое уравнение . Разложим левую часть на множители: . Следовательно, корни характеристического уравнения: . Поэтому общее решение исходного уравнения имеет вид: .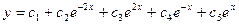

2. Корни уравнения (34.9) различны, среди них есть комплексные. При этом, как было показано ранее, они образуют пары комплексно сопряженных чисел. Решения уравнения (34.8), соответствующие паре комплексно сопряженных решений уравнения (34.9) и , имеют вид 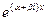и и могут быть заменены двумя действительными решениями: действительной и мнимой частями указанных решений. Следовательно, так как , решениями уравнения (34.8) будут и .

Пример.

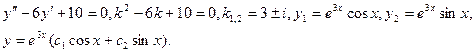
3. Характеристическое уравнение имеет кратные корни. В этом случае число линейно независимых решений предыдущих типов меньше п, и для получения фундаментальной системы нужно найти дополнительные решения иного вида. Докажем, что при наличии у характеристического уравнения корня k_i кратности α_i такими решениями будут 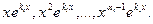Предположим вначале, что выбранный кратный корень k_i = 0. Тогда характеристическое уравнение имеет вид:

,

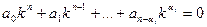а соответствующее дифференциальное уравнение:

.

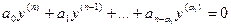Очевидно, что частными решениями такого уравнения будут функции 1, x, x ²,…, , все производные которых порядка α_i и выше равны нулю. Кстати, линейная независимость такой системы функций показана в одном из предыдущих примеров.

Пусть теперь корень характеристического уравнения k_i кратности α_i не равен нулю. Сделаем замену переменной: , тогда при подстановке в дифференциальное уравнение его линейность и однородность не нарушается, а коэффициенты изменяются, но по-прежнему остаются постоянными:

.

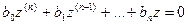При этом корни характеристического уравнения

(34.10)

отличаются от корней уравнения

на слагаемое – k_i, так как при 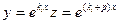, то есть k = k_i + p. Следовательно, уравнение (34.10) имеет корень р = 0 кратности α_i, которому соответствуют линейно независимые частные решения 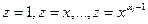. При обратной замене получаем набор линейно независимых решений исходного уравнения:

. (34.11)

Таким образом, каждый кратный корень уравнения (34.9) задает серию линейно независимых частных решений уравнения (34.8), количество которых равно его кратности. Следовательно, вновь построена фундаментальная система решений.

Замечание. Кратные комплексно сопряженные корни задают частные решения вида .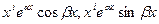

Примеры.

1. Характеристическое уравнение для уравнения имеет вид (k + 1)³ =0, то есть k = -1 – корень кратности 3. Следовательно, фундаментальная система решений состоит из функций , а общее решение можно записать в виде .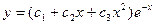

2. Для уравнения характеристическим уравнением является 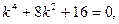то есть (k ²+4)²= 0. Следовательно, 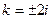- корни кратности 2. Тогда общим решением исходного дифференциального уравнения является

.

Неоднородные линейные дифференциальные уравнения.

Частное и общее решения.

Ранее было показано, что сумма решений линейного неоднородного уравнения L [ y ] = f(x) и соответствующего однородного уравнения L [ y ] = 0 является решением неоднородного уравнения. Используя это свойство, можно доказать следующую теорему:

Теорема 35.1. Общее решение на отрезке [ a,b ] уравнения L [ y ] = f(x) с непрерывными на [ a,b ] коэффициентами p_i(x) и правой частью f(x) равно сумме общего решения соответствующего однородного уравнения и какого-либо частного решения неоднородного уравнения.

Доказательство.

Требуется доказать, что для любых начальных условий , можно подобрать такие значения постоянных c_i, чтобы функция

, (35.1)

где y_i – линейно независимые частные решения однородного уравнения L [ y ] = 0, а 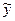- частное решение рассматриваемого неоднородного уравнения, была решением этого неоднородного уравнения с заданными начальными условиями. Это требование приводит нас к системе уравнений относительно неизвестных с ₁, с ₂,…, с_п:

, (35.2)

главным определителем которой является определитель Вронского , как известно, не равный нулю. Поэтому система (35.2) имеет единственное решение, что и доказывает утверждение теоремы.

Замечание. Таким образом, при найденном общем решении однородного уравнения решение неоднородного уравнения сводится к подбору его частного решения.

Методы нахождения частного решения неоднородного линейного дифференциального уравнения (метод вариации произвольных постоянных, метод неопределенных коэффициентов и принцип суперпозиции).

Распространим метод вариации произвольных постоянных, рассмотренный для решения линейного уравнения первого порядка, на линейные уравнения высших порядков. Будем искать решение неоднородного уравнения в виде 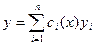. При этом требуется найти п неизвестных функций с ₁(х), с ₂(х),…, с_п (х), которые удовлетворяли бы только одному уравнению

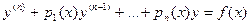. (35.3)

Поэтому можно дополнительно потребовать, чтобы искомые функции удовлетворяли еще каким-нибудь п- 1 уравнениям, выбранным так, чтобы производные функции 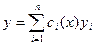имели по возможности такой же вид, как при постоянных c_i. Первая производная решения имеет вид: . Потребуем, чтобы вторая сумма в этом выражении равнялась нулю: , тогда . Зададим такое же условие для второй производной:

, , . Продолжая вычислять производные функции 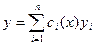до порядка п – 1 включительно и требуя каждый раз, чтобы , получим:

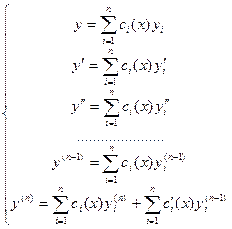(35.4)

(в последнем равенстве уже нельзя потребовать, чтобы вторая сумма равнялась нулю, так как на искомые функции уже наложено п – 1 условие, а последним требованием является то, что эти функции должны удовлетворять уравнению (35.3)). Подставив 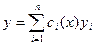с учетом (35.4) в (35.3), получим:

,

но y_i – частные решения однородного уравнения, следовательно, все слагаемые второй суммы равны нулю и уравнение сводится к следующему:

. (35.5)

Добавив его к первым п – 1 уравнениям системы (35.4), получим систему из п уравнений для определения с₁΄, с₂΄,…, с_п΄, определитель которой является определителем Вронского для функций у₁, у₂,…, у_п и, следовательно, не равен нулю. Следовательно, из этой системы можно единственным образом найти производные искомых функций, а затем с помощью интегрирования и сами функции с₁, с₂,…, с_п.

Пример.

. Найдем решение однородного уравнения, для чего составим характеристическое уравнение k ² - 2 k + 1 = 0, k₁ = k₂ = 1. Следовательно, общее решение однородного уравнения имеет вид у = (с₁ + c ₂ x) е^х, то есть фундаментальную систему решений составляют функции у₁ = е^х и у₂ = хе^х. Будем искать общее решение неоднородного уравнения в виде у = с₁ (х) е^х + с₂ (х) хе^х. Составим систему (35.4):

, откуда ,

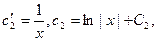
, где С₁ и С₂ – произвольные постоянные. Таким образом, найдено общее решение исходного уравнения: у = е^х (х ln| x | - x + C₁x + C₂).

Подбор частного решения для неоднородного уравнения с постоянными коэффициентами.

Для некоторых видов правой части линейного неоднородного дифференциального уравнения

(35.6)

можно подобрать частное решение в виде функции с неопределенными коэффициентами, которые определяются путем подстановки этой функции в уравнение (35.6).

1. f(x) = A₀ x^s +A₁ x^s-1 +…+ A_s (а_п ≠ 0).

При этом существует частное решение уравнения (35.6), имеющее такой же вид: y = B₀ x^s + B₁ x^s-1 +…+ B_s. Действительно, подставив эту функцию в уравнение (35.6) и приравняв коэффициенты при одинаковых степенях х, получим разрешимую единственным образом систему линейных уравнений: .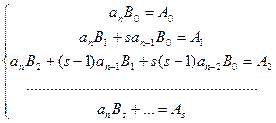

Пример.

.

Будем искать частное решение в виде у = Ах + В, тогда 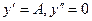, и после подстановки в уравнение получим: 3 А + 2 Ах + 2 В = 3 х – 5. Тогда 2 А = 3, 3 А + 2 В = = -5. Следовательно, 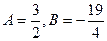, и общее решение уравнения можно записать в виде:

.

2. Если 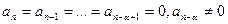(то есть k = 0 является α – кратным корнем характеристического уравнения), то частное решение имеет вид:

.

Легко убедиться, что функция подобного вида является решением уравнения (35.6) при поставленных условиях.

Пример.

.

Пусть

Подставляя в уравнение, получим: 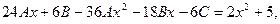откуда

–36 А = 2, 24 А – 18 В = 0, 6 В – 6 С = 5.

Решая эту систему, получаем Следовательно, общее решение уравнения имеет вид: .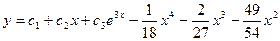

3. .

Если число р при этом не является корнем характеристического уравнения, можно задать частное решение в виде:

.

Если же р – корень характеристического уравнения кратности α, частное решение имеет вид: 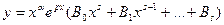. В обоих случаях с помощью подстановки в исходное уравнение можно убедиться, что выбранные функции являются его решениями.

Пример 1.

.

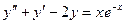Найдя корни характеристического уравнения k ² + k – 2 = 0: k₁ = 1, k₂ = -2, видим, что р = -1 не является корнем этого уравнения. Поэтому будем искать частное решение в форме

y = e^-x (Ax + B).

При этом 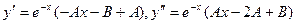. Подставляя в уравнение, получаем: , откуда –2 А = 1, - А – 2 В = 0, то есть . Итак, общее решение уравнения: .

Пример 2.

.

Здесь р = 1 – корень характеристического уравнения кратности 2, поэтому частное решение имеет вид 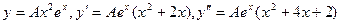. Подстановка в уравнение дает 2 Ае^х = 2 е^х, откуда А =1, а общее решение: у = (с₁ + с₂х + х ²) е^х.

4. В аналогичной форме задаются частные решения в случае, когда правая часть уравнения имеет вид , где Р и Q – некоторые многочлены:

а) если p ± qi - не корни характеристического уравнения, то можно подобрать частное решение в виде 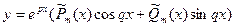, где и - многочлены с неопределенными коэффициентами, степень т которых есть старшая из степеней многочленов Р и Q.

б) если p ± qi - корни характеристического уравнения кратности α, то

.

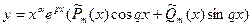Пример.

. При этом ±- корни характеристического уравнения кратности 2, поэтому следует искать частное решение в виде: .

5. Если правая часть уравнения (35.3) представляет собой сумму функций, рассмотренных в предыдущих пунктах, то по принципу суперпозиции частное решение будет задаваться как сумма решений, соответствующих каждому из слагаемых правой части.

Пример.

Для уравнения 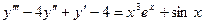частное решение ищем в виде:

.

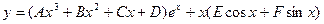Дата добавления: 2014-01-04