Ряды функций

Если каждая точка замкнутой и ограниченной области есть центр круга, то существует конечное число этих кругов, покрывающих область, т. е. таких, что всякая точка области лежит внутри, по крайней мере, одного из этих кругов.

Для доказательства заключим область 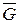внутрь квадрата 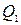со сторонами, параллельными осям координат, и разделим этот квадрат на четыре конгруэнтных квадрата. Предполагая утверждение неверным для области G, мы должны допустить, что оно неверно для множества точек области G, лежащих хотя бы на одном из этих четырёх квадратов.

Обозначим такой квадрат через 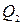и разделим его снова на четыре конгруэнтных квадрата; получим квадрат .

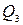Продолжая такое разделение дальше, мы получим последовательность квадратов 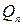, каждый из которых содержит часть области 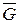, для которой наше утверждение неверно, т. е. для которой необходимо по­крытие бесконечно многими кругами 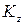. Пусть 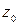есть точка, принадлежащая всем квадратам 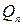. Если 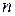достаточно большое, то в произвольной окрестности точки 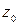лежат квадраты 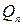и, следовательно, точки области 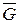. Таким образом, точка 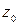при­надлежит сама области G и является, следовательно, центром круга 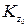. Обозначим радиус этого круга через 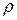. Выбирая 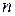столь большим, чтобы диагональ квадрата 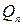была меньше 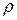, мы видим, что все точки области 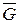, принадлежащие такому 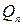, покрываются с помощью одного круга 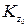, в то время как, по предположению, для покрытия этих точек необходимо бесконечное множество кругов системы 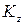. Полученное противоречие убеждает нас в справедливости леммы.

Замечание. Лемма, очевидно, остаётся верной, если вместо области 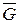возьмём непрерывную кривую или вообще любое ограниченное замкнутое множество точек плоскости.

Множество точек плоскости называется огра­ниченным, если оно целиком лежит в конечной части плоскости; оно назы­вается, сверх того, замкнутым, если содержит все свои предельные точки, т. е. точки 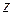плоскости, в произвольных окрестностях которых находятся точки множества, отличные от .

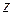Обращаясь к доказательству теоремы о равномерной непрерыв­ности, рассмотрим для каждой точки 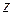области G круг с центром в 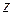радиуса 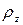такой, что для любых двух точек 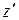и 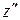, лежащих внутри этого круга, имеет место неравенство ; это следует непосредственно из непрерывности функции 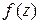в каждой точке 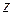области 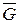. Как в лемме Гейне-Бореля, поставим в соответ­ствие каждой точке 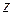области 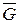круг с центром в этой точке радиуса 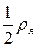. На основании леммы существует система конечного числа таких кругов, покрывающая область .

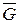Пусть радиус наи­меньшего среди этих кругов равен 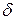; мы утверждаем, что это число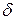удовлетворяет условиям доказываемой теоремы. В самом деле, если 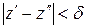и точка 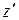лежит внутри круга с центром в точке 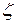радиуса 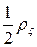, то 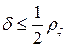и, следовательно, точк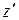и и 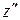лежат внутри круга с центром в точке 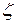радиуса ; отсюда следует: , что и требовалось доказать.

Дата добавления: 2014-01-04