Понятие наибольшего предела

Пустьдана последователь­ность действительных неотрицательных чисел:

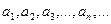(40.3.)

Может случиться, что последовательность чисел (40.3.) неограниченная, т. е. среди чисел (40.3.) найдутся числа, больше любого задан­ного положительного числа. В этом случае условимся говорить, что наибольший предел 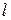последовательности чисел (40.3.) равен 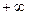. Второй случай будет тот, когда последовательность чисел (40.3.) огра­ниченная, , т.е. все точки, изображающие числа (40.3.), лежат на конечном отрезке 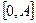. Как мы знаем, ограниченная последова­тельность точек имеет по крайней мере одну предельную точку; вообще говоря, множество всех предельных точек нашей последовательности (40.3.) будет бесконечным множеством (обо­значим его через 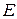), лежащим на отрезке 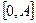. Когда мы имеем конечное число точек отрезка,то среди них имеется одна точка, лежащая правеевсех остальных. В случае бесконечного множества точек, расположенных на конечном отрезке, может случиться, что у множества нет самой правой точки. Например, множество точек отрезка не имеет точки, которая была бы расположена правее всех остальных. Однако такого обстоятель­ства не может быть для рассматриваемого множества 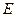предельных точек.

Действительно, легко показать, что среди точек множества 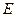предельных точек ограниченной последовательности (40.3.) существует точка, лежащая правее всех остальных. С этой целью разделим отре­зок 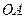, который мы обозначим через 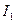пополам, и пусть есть его середина. Возможно одно из двух: либо отрезок содержит бесконечное множество точек данной последовательности, либо нет. В первом случае за второй отрезок 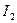примем , во втором слу­чае . 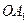Подобно отрезку 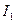отрезок 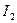содержит бесконечное мно­жество точек данной последовательности.

Затем снова делим пополам отрезок 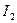, и если правая его половина содержит бесконечное мно­жество точек данной последовательности, то за отрезок 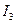принимаем правую его половину, а если правая половина отрезка 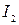содержит конечное число точек последовательности [в частности, совсем лишена точек (40.3.)], то за отрезок 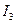принимаем левую половину отрезка 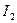. Продолжая этот процесс неограниченно, получим бесконечную после­довательность отрезков 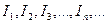таких, что каждый отрезок принадлежит предыдущему, причём длина отрезка , равная 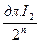, стремится к нулю, когда я неограниченно возрастает.

Кроме того, отметим, что всякий отрезок содержит бесконечное множество точек данной последовательности, причём правее его может находиться лишь конечное число таких точек.

На основании принципа вложенных отрезков существует точка, общая всем отрезкам , которую мы обозначим через .

Докажем теперь, что есть самая правая предельная точка данной последовательности. Для этого мы покажем, во-первых, что никакая точка, лежащая правее , не может быть предельной точкой для данной последовательности и, во-вторых, что . есть предельная точка. Действительно, пусть лежит правее ,. Выбирая 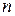доста­точно большим, мы можем считать, что точка лежит правее отрезка . Но вправо от отрезка может находиться лишь конеч­ное число точек данной последовательности и, следовательно, точка не может для неё быть предельной. Сама же точка , очевидно, есть предельная для данной последовательности, потому что произ­вольная окрестность этой точки содержит отрезок (если я доста­точно велико), на котором лежит бесконечное множество точек данной последовательности.

Итак, множество 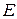предельных точек ограниченной последова­тельности (40.3.) имеет точку, лежащую правее всех остальных точек множества .

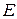Число, соответствующее этой «самой правой» предель­ной точке, будет предельным числом данной последовательности чисел (40.3.), наибольшим среди всех предельных чисел этой последо­вательности.

Таким образом, мы доказали существование конечного числа 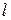, наибольшего среди предельных чисел ограниченной последо­вательности (40.3.) неотрицательных чисел. Согласно предыдущему вся­кая последовательность неотрицательных чисел имеет наибольший предел 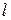, конечный или равный 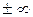, т. е. .

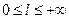Символи­чески это записывают так: .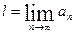

Так как любое предельное число последовательности неотрицательных чисел не меньше нуля, то в случае 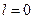данная последовательность чисел (40.3.) должна схо­диться к нулю.

Дата добавления: 2014-01-04