Теорема о моменте количества движения

Пусть точка М массы движется по некоторой кривой под действием силы 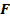(рис.20.2).

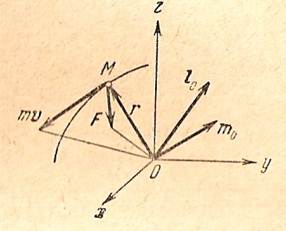Рис.20.2.

Построим вектор , изображающий момент силы 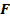относительно начала координат О. Этот вектор направлен перпендикулярно плоскости треугольника, который получим, соединив начало и конец вектора, 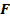с точкой О. По модулю он равен удвоенной площади этого треугольника. Проекции этого вектора на координатные оси равны моментам силы относительно этих осей.

Момент силы 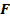относительно точки О можно представить в виде векторного произведения радиуса вектора точки М на эту силу:

Построим вектор , изображающий момент количества движения относительно данной точки О в виде векторного произведения радиуса вектора на вектор :

Между моментом количества движения относительно данной точки и моментом относительно какой-нибудь оси, проходящей через эту точку, существует такая же зависимость, как и между моментами силы 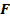. Поэтому проекции вектора на координатные оси равны моментам количества движения относительно этих осей:

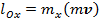
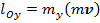
Известны следующие формулы для моментов силы относительно координатных осей:

Где 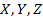- проекции силы 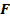на оси, а х, у, z – координаты точи приложения этой силы.

Моменты количества движения относительно координатных осей мы можем вычислить по этим формулам, заменив проекции вектора 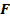проекциями вектора на те же оси:

Найдем зависимость между векторами и .

Дифференцируя по времени момент движения относительно точки О, получим:

Но

Следовательно:

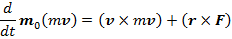
Но так как векторы 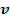и направлены по одной прямой, то

Т.е.

Или

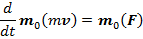
Производная по времени от момента количества движения материальной точки относительно какого-нибудь неподвижного центра О равна моменту действующей на эту точку силы относительно того же центра.

Представим полученное равенство в виде:

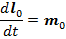
И спроектируем это равенство на координатные оси. Так как проекция производной от данного вектора на какую-нибудь ось равна производной от проекции этого вектора на ту же ось:

Или

Эти уравнения выражают теорему о моменте количества движения в координатной форме:

Производная по времени от момента количества движения материальной точки относительно какой-нибудь неподвижной оси равна моменту действующей на эту точку силы относительно той же оси.

Следствия:

1. Пусть момент, действующий на материальную точку силы относительно оси z, во все время движения остается равным нулю, т.е. . Тогда будем иметь:

Следовательно, , т.е. если момент действующей силы относительно какой-либо неподвижной оси вес время равен нулю, то момент количества движения материальной точки относительно этой оси остается постоянным.

2. Пусть линия действия силы 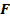во все время движения проходит через одну неподвижную точку О. В этом случае сила называется центральной, а точка О называется центром этой силы. Тогда и, следовательно: и

В случае центральной силы момент количества движения материальной точки относительно центра этой силы остается постоянным. Под действием центральной силы точка всегда описывает плоскую траекторию, плоскость которой проходит через центр этой силы.

Дата добавления: 2014-01-04