Излучение электромагнитной энергии

ИЗЛУЧЕНИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ В НАПРАВЛЯЮЩИХ СТРУКТУРАХ

ЛЕКЦИЯ № 44

Упражнения.

Решить следующие линейные однородные дифференциальные уравнения:

1) 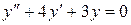. Ответ: .

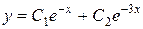2) 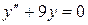. Ответ: .

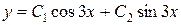3) 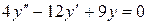. Ответ: .

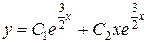Рассмотрим вопрос об излучении электромагнитной энергии элементом тока. Пусть по отрезку проводника длиной 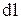, находящемуся в воздухе (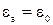, 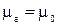), протекает ток 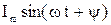(рисунок 1). Далее будем пользоваться цилиндрической и отчасти сферической системами координат. Ось z цилиндрической системы направим вдоль проводника. Пусть положительное направление тока по проводнику совпадает с положительным направлением оси z.

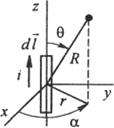
Рисунок 1

Найдем значение вектор-потенциала в произвольной точке, удаленной от элемента тока на расстояние R. В соответствии с

,

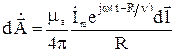или, если исключить множитель ,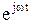

.

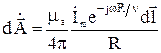Направление 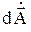совпадает с направлением вектора 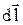(вдоль оси z). Найдем магнитную индукцию в произвольной точке поля: 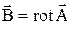. Раскроем ротор в цилиндрической системе координат:

.

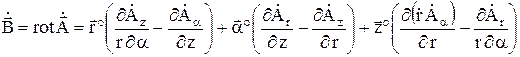Так как 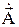имеет единственную составляющую 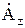и она зависит только от R и в силу симметрии поля не зависит от α, то

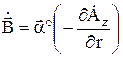. (1)

Из формулы (1) следует, что магнитная индукция имеет α-е направление. Для нахождения комплекса магнитной индукции надо вычислить 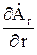; 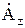зависит в явном виде от R, а не от r. Поэтому

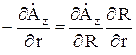. (2)

Для любой точки пространства справедливо, очевидно, вытекающее из теоремы Пифагора соотношение

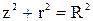. (3)

Продифференцируем (3) по r, получим

.

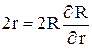Следовательно,

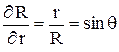. (4)

Составляющая 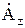состоит из произведения двух функций R: 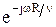и 1/R. Поэтому

,

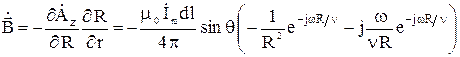или

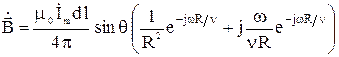. (5)

Выражение (5) можно переписать и в ином виде, перейдя к мгновенным значениям:

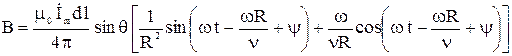. (6)

Формула (6) позволяет сделать вывод, что в любой точке пространства магнитная индукция от элемента переменного тока имеет две составляющие, одна из них убывает обратно пропорционально квадрату радиуса и изменяется по закону синуса во времени, другая убывает обратно пропорционально первой степени радиуса и изменяется по закону косинуса во времени.

Найдем закон изменения напряженности электрического поля. В соответствии с первым уравнением Максвелла

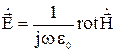. (7)

Так как 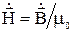, то

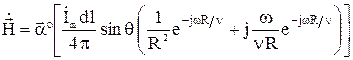. (8)

Далее целесообразно перейти к сферической системе координат. Проекции 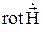в сферической системе следующие:

;

;

.

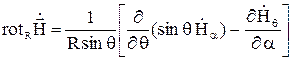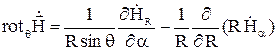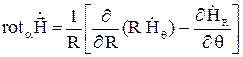Так как 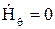, , 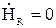то

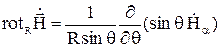; (9)

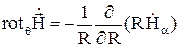. (10)

Найдем проекцию 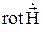на направление R:

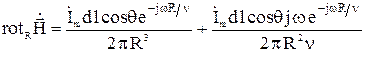. (11)

В свою очередь проекция 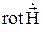на направление θ по формуле (10)

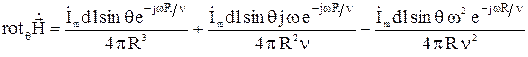. (12)

Для того чтобы получить проекции 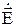на направления R и θ, необходимо соответствующие проекции 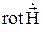разделить на 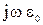(7):

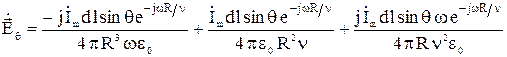; (13)

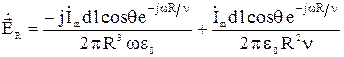. (14)

Таким образом, напряженность электрического поля имеет две составляющие: одна направлена по θ, другая – по R; 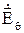содержит три слагаемых (13), изменяющихся обратно пропорционально соответственно третьей, второй и первой степеням расстояния R; 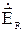состоит из двух слагаемых, изменяющихся обратно пропорционально 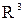и 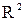. Частное

.

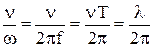Отношение модуля первого слагаемого в (11) к модулю второго равно 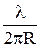(λ – длина волны).

Если 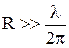, то первым слагаемым по сравнению со вторым можно пренебречь; если 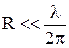, то, наоборот, можно пренебречь вторым слагаемым. Аналогичные соотношения имеют место между модулями слагаемых в (12).

Принято все поле делить на ближнюю, среднюю и дальнюю зоны. Для ближней зоны 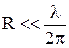; для дальней 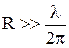. В средней зоне 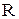соизмеримо c .

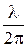В соответствии с этим для ближней зоны

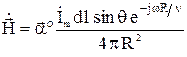; (15)

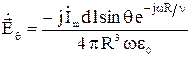; (16)

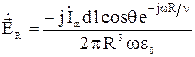, (17)

для дальней зоны

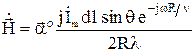; (18)

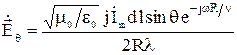; (19)

Запишем мгновенные значения Н и Е для дальней зоны:

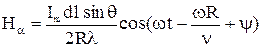; (20)

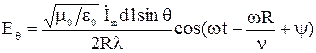. (21)

Таким образом, в дальней зоне, т.е. в зоне, для которой 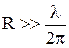напряженность магнитного поля имеет только одну α-составляющую, а напряженность электрического поля – только одну θ-составляющую (18) – (19). Если провести сферу радиусом R, то во всех точках этой сферы (назовем ее эквифазной поверхностью) H имеет одну и ту же фазу колебания в какой-то конкретный момент времени (фаза колебания определяется аргументом косинуса). Амплитуда Н для точек сферы 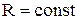различна, она зависит от угла θ; на «полюсах» при θ = 0 и при θ = 180° амплитуда колебания для любого момента времени равна нулю, так как 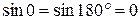, амплитуда колебания максимальна на «экваторе» сферы при θ = 90°. По фазе Н и Е совпадают (20) – (21). Модуль Е в 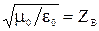раз больше модуля Н, т. е. .

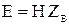Диаграмму зависимости модуля Е и Н в дальней зоне от угла θ принято называть диаграммой направленности. Она будет представлять собой объемную фигуру – тор, сечение которого плоскостью, проходящей через полярную ось, представляет собой две соприкасающиеся окружности (рисунок 2, а).

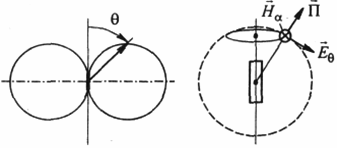
а б

Рисунок 2

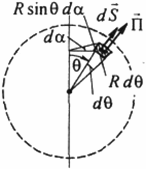
Рисунок 3

Составим выражение вектора Пойнтинга для дальней зоны: 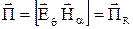. Векторное произведение двух векторов, один из которых имеет θ-е направление, а другой – α-е, дает вектор 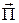, направленный по радиусу (рисунок 2, б). Так как Н и Е в дальней зоне совпадают по фазе, то с изменением направления Н на противоположное (Н изменяется во времени по косинусоиде) одновременно меняется на противоположное и направление вектора Е. Но вектор 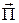своего направления не меняет, он все время направлен вдоль радиуса.

Найдем модуль вектора Пойнтинга. С этой целью умножим модуль Е на модуль Н:

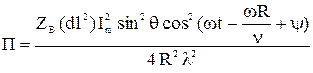. (22)

Среднее значение модуля вектора Пойнтинга за период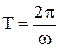

.

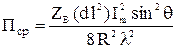Подсчитаем поток вектора Пойнтинга через сферическую поверхность радиусом R. Элемент 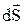сферической поверхности радиусом R направлен по радиусу. Вектор Пойнтинга 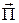также направлен по радиусу. Угол между ними равен нулю (рисунок 3).

Элемент сферической поверхности можно рассматривать как криволинейный квадрат, площадь его (рисунок 3):

;

;

.

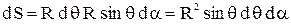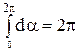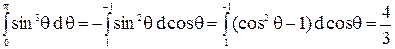Заменим 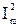на 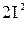(I – действующее значение тока). В результате окажется, что поток вектора Пойнтинга через сферическую поверхность радиусом R, представляющий собой мощность 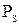, излученную элементом тока, не зависит от радиуса и равен

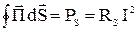, (23)

где

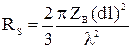. (24)

Величину 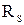называют сопротивлением излучения. Чем больше 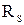, тем больше излученная мощность при том же токе I. Сопротивление излучения прямо пропорционально квадрату длины излучателя и обратно пропорционально квадрату длины волны λ.

Так как длина волны 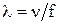, то излученная мощность прямо пропорциональна квадрату частоты. Если частота мала, например всего 50 Гц, то излучения практически нет. При радиочастоте излучение значительно. Например, при частоте 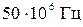излучение больше, чем при частоте 50 Гц, в 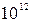раз.

Дата добавления: 2014-01-04