Основы многокритериальной оптимизации

УЧЕБНЫЕ ВОПРОСЫ И РАСЧЕТ ВРЕМЕНИ

Воспитывать творческий подход и настойчивость при изучении дисциплины

Рассмотреть общую схему решения многокритериальных задач.

УЧЕБНЫЕ И ВОСПИТАТЕЛЬНЫЕ ЦЕЛИ

Занятие № 39. Многокритериальные задачи принятия решений.

Тема № 9. Многокритериальные задачи ТПР.

Теория принятия решений

По учебной дисциплине

ЛЕКЦИЯ

Обсуждено на заседании ПМК

"___" августа 2009 г.

Протокол № 1

1. Изучить общую постановку задачи многокритериальной оптимизации.

Время: 2 часа. Место: Аудитория.

МАТЕРИАЛЬНОЕ ОБЕСПЕЧЕНИЕ:

Литература : Орлов А.И. Теория принятия решений.Учебник.. М., «Экзамен», 2006.

Наглядные пособия: дидактический материал (слайды).

Технические средства обучения: “Лектор–2000”.

I.	Введение		мин.
II.	Учебные вопросы
	1. Основы многокритериальной оптимизации.		мин.
	2. Общая схема решения многокритериальных задач.		мин.
III.	Заключение		мин.

ВВЕДЕНИЕ

Проверить наличие студентов и их готовность к занятию.

Объявить студентам о том, что они начинают изучение темы «Многокритериальные задачи ТПР», играющей важнейшую роль в теории принятия решений. Довести до студентов, что данная тема включает 8 часов аудиторных занятий, из которых 4 часа лекций, 2 часа практических занятий и 2 часа лабораторных работ. Следующее за лекцией 2-х часовое практическое занятие будет посвящено освоению методов решения многокритериальных задач.

МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ПО ИЗЛОЖЕНИЮ УЧЕБНЫХ ВОПРОСОВ

При изложении первого вопроса перечислить основные понятия и определения многокритериальной оптимизации. Изложение учебного материала проводится с элементами диалогового метода, при этом студентам задается следующий вопрос: ´ В чем причина возникновения многокритериальности в ТПР?

При изложении второго вопроса рассмотреть общую схему решения многокритериальных задач. Изложение учебного материала проводится с элементами диалогового метода, при этом студентам задается следующий вопрос: ´ Что задает паретовское множество?

Вся сознательная жизнь человека связана с принятием решений. Одни решения касаются только самого принимающего решения, другие относятся к небольшому кругу людей, третьи затрагивают интересы целой организации, региона и даже страны. Чем выше уровень, тем серьезнее могут быть последствия, тем выше ответственность принимающих решения. Усложнение ситуаций, в которых приходится принимать решения, вызвало потребность в научной поддержке, что привело к развитию нового подхода, получившего название исследование операций. Однако до начала семидесятых годов в рамках исследования операций рассматривались в основном задачи, в которых эффективность решения оценивалась одним критерием. В то время считалось, что требования, предъявляемые к решению, можно выразить одним показателем качества. Методы математического программирования, интенсивно развиваемые в исследовании операций, изначально ориентировались на решение однокритериальных задач.

Со временем росло понимание неадекватности такого подхода реальным процессам принятия решений. Все яснее становилась необходимость учитывать существование более одного показателя эффективности, оптимальные решения по которым не совпадают. С этого периода началось бурное развитие многокритериальных методов принятия решений и, в частности, методов многокритериального математического программирования.

Многокритериальность может быть обусловлена одной из трех причин:

1. Цель не может быть адекватно представлена (покрыта) одним критерием.

2. Принимающий решения ставит более одной цели, которые связаны общими активными средствами.

3. Решения принимаются группой лиц с несовпадающими интересами.

Так для характеристики цели «Повысить уровень жизни народа» требуется целый ряд показателей. При выборе номенклатуры и количества выпускаемых изделий начинающая фирма может преследовать как тактическую цель – получение высокой прибыли в ближайшее время, так и стратегическую – закрепление на рынке сбыта и его расширение. В качестве примера третьей ситуации можно привести переговоры России и Казахстана по космодрому Байконур.

В формальном представлении критерии (целевые функции), по которым оценивается решение Х, будет записываться в виде fi(Х), .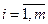

Критерий fi называют также частными. Для удобства рассуждений примем, что для всех i чем больше значение критерия, тем лучше. Тогда задача многокритериального математического программирования запишется в виде:

max{ f ₁(X)= y ₁},

max{ f ₂(X)= y ₂},

.......

max{ f_m (X)= y_m },

Х 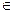D,

где D – множество допустимых решений. Иначе говоря, задача состоит в максимизации вектора критериев f(X)=Y по X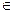D.

Существенное отличие этой задачи от традиционной однокритериальной состоит в понятии оптимальности. В однокритериальной задаче под оптимальным понимается решение, обеспечивающее максимальное значение критерия. При многих критериях увеличение одних критериев приводит к уменьшению других (редкие исключения не представляют практического интереса) и поэтому понятие оптимальности требует принципиальных уточнений. Очевидно, что без дополнительной информации о предпочтениях ЛПР бессмысленно говорить об оптимальном решении и тем более формализованно искать его.

Допустимое множество D строится в n-мерном пространстве переменных. Каждое решение X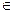D полностью характеризуется соответствующими значениями всех частных критериев, т.е. вектором Y. Числовое m-мерное пространство Em, координатами которого являются yi=fi(X), называется критериальным пространством. Очевидно, что каждому Х можно поставить в соответствие точку в критериальном пространстве. Если же решение Х допустимо, то соответствующая точка в Em, определяемая вектором Y, является достижимой. Множество таких точек в критериальном пространстве называется множеством достижимости (достижимых векторов). Таким образом, векторная функция f(X) отображает допустимое множество D на множестве достижимости G:

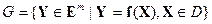
и задача состоит в выборе вектора из этого множества, наилучшего с точки зрения ЛПР.

В общем случае построение множества G для реальных задач весьма проблематично, но для задач с «хорошими» свойствами, например, линейных, множество достижимости может быть построено.

Как отмечалось выше, без установления принципа оптимальности, отражающего предпочтения ЛПР, невозможно формально распознать оптимальное решение (как в сказке: "ищи то, не знаю, что"). Однако учитывая стремление ЛПР к увеличению значений всех частных критериев, можно формальными методами исключить из множества G (и D) заведомо не перспективные точки и тем самым облегчить решение задачи.

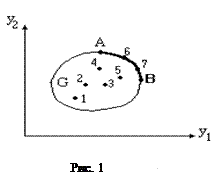Для наглядности рассуждений рассмотрим пример с двумя критериями (рис 1). Независимо от предпочтений ЛПР, вектор критериев, соответствующий точке 2, лучше, чем в точке 1. Аналогично, точка 3 лучше точки 2, а 4 лучше 3. Но точки 4 и 5 оказываются не сравнимыми, так как по первому критерию лучше точка 5, а по второму – точка 4. Как для точки 5, так и для 4 на множестве G можно найти лучшую точку, например 6. Нетрудно убедиться в том, что для любой точки Y внутри G найдется точка, которая ее доминирует, т.е. лучше хотя бы по одному частному критерию и не хуже по всем другим. В то же время для точек 6 или 7 этого сделать нельзя. Более того, не найдется вектора из G, который доминировал бы точку, принадлежащую северо-восточной границе AB множества G. Таким образом, векторы на АВ являются недоминируемыми (неулучшаемыми). Одновременно они являются несравнимыми между собой (например, в точках 6 и 7), поэтому отдать предпочтение одному из них без ЛПР невозможно. Такие точки (векторы критериев и соответствующие решения) называют эффективными или оптимальными по Парето. Их совокупность образует множество Парето (паретовское множество).

Это наименование произошло от фамилии итальянского экономиста и социолога В.Парето (1848-1923), который проводил математические исследования процесса рыночного обмена товаров. Рассматривалась модель чистого обмена, в которой каждый участник стремится составить себе набор товаров наибольшей ценности. Эффективным является такое состояние, которое не может быть улучшено путем перераспределения товаров ни для одного из участников без ущемления интересов некоторых других участников. Значит, эффективное состояние соответствует экономическому равновесию, а неэффективное состояние побуждает проводить перераспределение (торговать), которое ведет к установлению равновесия.

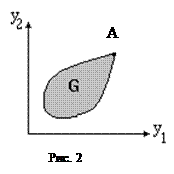Теперь очевидно, что оптимальное решение следует искать только среди эффективных точек. При групповом принятии решений множество эффективных точек называют также переговрным, подчеркивая тем самым, что только их и нужно рассматривать в качестве претендентов на компромиссное решение. Если эффективная точка одна (А на рис.10.2), что возможно в тривиальном случае непротиворечивости критериев, то она и является искомым оптимумом. В задачах с конечным числом точек G (дискретные задачи) выделение эффективного множества часто настолько уменьшает число вариантов, что выбор из них наилучшего не вызывает затруднений у ЛПР.

Однако при непрерывном и тем более невыпуклом множестве G паретовское множество имеет сложную структуру и его исследование требует специальных методов

Ввиду особой важности парето-оптимальности для решения многокритериальных задач приведем более строгие определения, связанные с этим понятием.

Дата добавления: 2014-01-04