Решение уравнений аналитическими методами

Решить любое уравнение y(x)=0 можно аналитически, символьно или с помощью встроенных стандартных функций. Для этого в SMath Studio предназначены следующие функции.

Функцию polyroots (рис. 5) можно использовать для нахождения корней полинома степени n, имеющего вид

a_nxⁿ +... + a₂x² +a₁x + a₀.

Эта функция не требует начального приближения и возвращает сразу все n корней, как вещественные, так и комплексные.

Коэффициенты полинома находятся в векторе A длины n + 1, который задается в качестве параметра функции polyroots(A) (рис. 5).

Рис. 5

Решение уравнения (5) с помощью данной функции представлено на рис. 6, из которого следует, что наша оценка корней по графику (рис. 1) была верной.

Рис. 6

Одним из распространенных методов решения уравнения является символьный метод, реализуемый следующим образом (рис. 7):

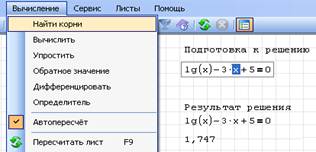
Рис. 7

1) задать само уравнение, причем знак равенства в нем задать комбинацией клавиш ctrl + =. Полученный жирный знак равенства называют Булево равенство;

2) в уравнении выделить идентификатор переменной, относительно которой следует решить это уравнение. Если такая переменная находится в уравнении в нескольких местах, то достаточно выделить ее только в одном месте;

3) перейти в основное меню и выполнить команды Вычисление /найти корни. Ниже уравнения появится решение.

Символьный метод определяет как действительные, так и комплексные корни.

Задания 3,4. Студентам выполнить решение двух предыдущих примеров, а также решить уравнения в соответствии с заданным вариантом.

Дата добавления: 2014-01-04