Точкових оцінок параметрів розподілу

Застосування методу моментів для визначення

Розглянемо методи визначення точкових оцінок, застосування яких дозволяє забезпечити виконання вимог, яким повинні відповідати статистичні оцінки. Найбільш поширеним для визначення точкових оцінок вибіркової сукупності є метод моментів. Він ґрунтується на тому, що невідомий параметр розподілу визначається рівнянням, яке утворюється, якщо прирівняти емпіричний момент, який обчислено за вибірковими даними, до відповідного теоретичного моменту розподілу випадкової величини, що розглядається. Такий підхід є можливим, оскільки початкові і центральні емпіричні моменти є ґрунтовними оцінками теоретичних початкових і центральних моментів того ж порядку.

Розглянемо оцінювання одного параметру розподілу за методом моментів. Нехай задана щільність ймовірностей 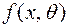, яка визначається одним невідомим параметром 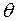. Необхідно визначити точкову оцінку цього параметру.

Для оцінювання одного параметру достатньо мати лише одне рівняння відносно цього параметру. Відповідно до методу моментів укладемо рівняння за умовою, що емпіричний початковий момент першого порядку дорівнює теоретичному початковому моменту першого порядку. Враховуючи те, що емпіричний початковий момент першого порядку є вибірковою середньою, а теоретичний – математичним сподіванням, записуємо умову для визначення невідомого параметру розподілу:

. (11.2)

За означенням математичного сподівання для неперервної випадкової величини маємо:

.

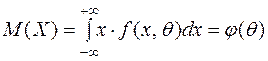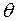Отже, математичне сподівання випадкової величини є певною функцією від параметра . Розв’язавши рівняння (11.2) відносно 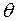, визначимо точкову оцінку цього параметру 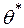. Оскільки ця точкова оцінка є функцією вибіркової середньої, то, відповідно, вона є функцією варіант, які утворюють вибіркову сукупність: .

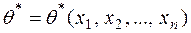Приклад. Відомо, що випадкова величина розподілена за показниковим законом. За даними вибіркової сукупності обчислили вибіркову середню цієї випадкової величини: 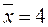. Визначити точкову оцінку параметра цього розподілу.

Розв’язання. Відомо, що показників закон розподілу випадкової величини описується функцією щільності ймовірностей, яка має вигляд:

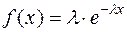, де .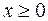

Для цієї випадкової величини . Отже, з рівнянням (11.2) маємо:

.

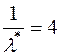
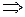
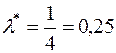Ми отримали, що точкова оцінка параметру розподілу дорівнює .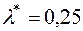

Тепер розглянемо оцінювання двох параметрів розподілу за методом моментів. Нехай задана щільність розподілу 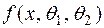, яка визначається двома невідомими параметрами 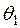і . Необхідно визначити точкові оцінки кожного з параметрів за статистичними даними.

Для оцінювання двох параметрів розподілу необхідно мати два рівняння відносно цього параметру. За методом моментів укладемо ці рівняння, наприклад, за умовою, що емпіричний початковий момент першого порядку дорівнює теоретичному початковому моменту першого порядку, а емпіричний центральний момент другого порядку дорівнює теоретичному центральному моменту другого порядку.

З урахуванням того, що теоретичний центральний момент другого порядку є дисперсією випадкової величини, а емпіричний центральний момент другого порядку є вибірковою дисперсією, отримуємо систему рівнянь:

(11.3)

Оскільки математичне сподівання і дисперсія є функціями від параметрів 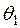і , розв’язавши цю систему відносно цих параметрів, ми отримаємо їх точкові оцінки. Ці статистичні оцінки є функціями варіант:

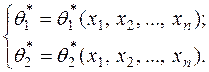
Приклад. За даними дослідження вибіркової сукупності, що містить 65 значень неперервної випадкової величини, розподіл якої у генеральній сукупності можна вважати рівномірним, проведено угрупування і за цими результатами побудовано інтервальний варіаційний ряд, який представлено в таблиці.

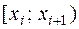
	[6,15; 6,65)	[6,65; 7,15)	[7,15; 7,65)	[7,65; 8,15)	[8,15; 8,65)	[8,65; 9,15)	[9,15; 9,65)	[9,65; 10,15)	[10,15; 10,65)	[10,65; 11,15)	[11,15; 11,65)

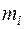
Визначити параметри розподілу випадкової величини, якщо з теоретичних міркувань можна вважати, що вона розподілена за рівномірним законом.

Розв’язання. Оскільки розподіл частот за інтервалами схожий на рівномірний, то нема підстав вважати теоретичне припущення хибним. Для рівномірного закону розподілу, оскільки саме таким вважається розподіл відповідно до теоретичних міркувань, функція щільності ймовірностей має вигляд:

Отже, необхідно визначити параметри і 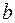цього розподілу.

Насамперед за вибірковими даними обчислимо статистичні оцінки математичного сподівання та дисперсії (пропонуємо зробити це самим). Отже, отримуємо: ; .

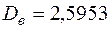Введемо поправку на зсув і, відповідно, отримаємо значення виправленої дисперсії:

.

Оскільки для рівномірного закону основні числові характеристики визначаються співвідношеннями: та 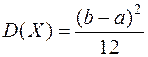, то з системи рівнянь (11.3) отримуємо формули для визначення точкових статистичних оцінок параметрів рівномірного розподілу:

(11.4)

Звідси 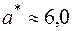та .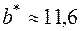

Дата добавления: 2014-01-04