Власні значення та власні вектори лінійного простору

Лекція 12

1. Власні вектори та власні значення

2. Ядро та образи лінійного оператора

Означення. Множина векторів лінійного простору x є L для яких Ax = 0 називається ядром лінійного простору.

Множина векторыв ӯ=Ах̄ називається образом лінійного оператора, або областю значень цього оператора.

Rer A – ядро

Im A (∮(A)) – множина образів

Ядро і образ утворюють підпростори у просторі L, при цьому вимірність ядра називається дефектом оператора А, а вимірність образу – рангом оператора А.

defA = dimRerA

RgA = rangA = dim ImA

Твердження. Для n-вимірного простору має місце рівність: dimRerA+rgA = n

Приклад. Знайти ядро та образ лінійного оператора А, який задано у деякому базисі матрицею:

-1 2 3

А = 1 1 0

0 3 3

За означенням ядра маємо:
Нехай х̄ =(х₁,х₂,х₃)

Підставимо:

-1 2 3 х₁

Ах̄ = 1 1 0 х₂

0 3 3 х₃

Або в розгорнутому вигляді

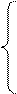-х₁+2х₂+3х₃=0

Х₁+х₂ =0

3х₂+3х₃=0

Система однорідна, лінійно знайдемо її ранг.

-1 2 3 -1 2 3 -1 2 3

1 1 0 0 3 3 0 1 1

0 3 3 0 3 3 0 0 0

RgA= 2

х₃=х₃ - параметр х₃=х₃

Х₂=-х₃ х₂=-х₃

-х₁=-2х₂-3х₃ Х₁=х₃

Нехай х₃=const, тоді х₂=-с, х₁=с.

RerA = (c;-c;c), де всі c є R

DimRerA = n-rgA

DimRerA= 3-2 = 1

Запишемо базис ядра:

Rer A = -1

Знайдемо образ оператора А, даного простору

ӯ =Ах̄

-1 2 3 х₁ у₁ -х₁+2х₂+3х₃ -1 2 3

у = 1 1 0 х₂ = > у₂ = х₁+х₂ = х₁ 1 +х₂ 1 +х₃ 0

0 3 3 х₃ у₃ 3х₂+3х₃ 0 3 3

Остання рівність говорить про те, що образ оператора А збігається з лінійною оболонкою системи стовпців матриці, тобто за базис образа може бути вибраний будь-який з базисів системи стовпців. Помічаємо, якщо додати відповідні елементи першого та третього стовпців то отримаємо другий стовпець, тобто дані стовпці лінійно незалежні, тобто вони утворюють базис образа, тому запишемо:

dimImA = 2

Базис складається з векторів:

-1 3

ImA: E₁ 1 E₂ 0

0 3

Означення. Не нульовий вектор х̄ називається власним вектором лінійного оператора А, якщо існує таке число λ, що задовольняє умову: Ах̄=λх̄ при цьому λ називається власним значенням лінійного оператора А, що відповідає власному вектору х̄.

Нехай деякому простору оператора А відповідає матриця А, а вектору х̄ - матриця стовпець з координатами цього вектора. Ах̄-λх̄ = 0

Зробимо перетворення.

(А-λ·Е)х̄ = 0 (1)

Запишемо в розгорнутому вигляді.

(a₁₁-λ)x₁+a₁₂x₂+ … + a_1nx_n = 0

a₂₁x₁+(a₁₁-λ)x₂+ … + a_2nx_n = 0 (2)

a_n1x₁+ … +(a_nn-λ)x_n = 0

Для існування нульового розв’язку необхідно, щоб визначник системи дорівнював 0.

(a₁₁-λ) a₁₂ a_1n

a₂₁ a₂₂-λ a_2n = 0 (3)

a_n1 … (a_nn-λ)

Вираз (3) називається характеристичним рівнянням. Ліва його частина є многочлен n-того порядку відносно λ, а корені характеристичного рівняння є власними значеннями лінійного оператора.

Сукупність усіх власних значень називається спектром лінійного оператора, при чому кожне власне значення входить у спектр стільки разів, яка його кратність.

Спектр буде простим якщо корені прості, дійсні.

Щоб знайти власні значення та власні числа необхідно:

1. розв'язати (3) і знайти λі

2. для кожного λ розв’яжемо систему рівнянь (2).

Будь-який не нульовий вектор α₁, α₂, … αn визначає власний вектор з власними значеннями λ.

Зауваження. Власні значення та власні вектори лінійного оператора називається також власним значенням та власними векторами матриці А цього оператора в даному базисі.

Якщо λ-власне значення і rg виразу (3) = r то існує n-r лінійно незалежних власних векторів оператора А. Тому, що вимірність простору відповідної однорідної системи дорівнює n-r.

Приклад. Знайти власні значення та власні вектори лінійного простора А, що задано матрицею:

1 2

А =

2 1

1) ∆ = |A-λE| = 0

1-λ 2

= 0

2 1-λ

1-λ²-4 = 0

(1-λ-2)(1- λ+2) = 0

- λ-1 = 0 - λ = -3

λ₁ = -1 λ₂ = 3

2) Знайти власні вектори

x₁ = -1

(1- λ)x₁+2x2 = 0

2x1+(1- λ)x2 = 0

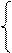2x₁+2x₂ = 0 |:2 x₁+x₂ = 0 x₁ = -x₂

2x₁+2x₂ = 0 x₂ = x₂ x₂ = x₂

Нехай x_i = C

x₁ = -C

тоді власний вектор:

xλ₁ = (-C, C) = C(-1, 1)

3) λ₂ = 3

-2x₁+2x₂ = 0 |:2 x₁-x₂ = 0 x₁ = x₂

2x₁-2x₂ = 0 |:2 x₂ = x₂ x₂ = x₂

Нехай x₂ = C

x₁ = C

xλ₂ = (C, C) = C(1, 1)

Приклад 2. Знайти λ, xλ_і

2 0 -1

А = 1 1 -1

-1 0 2

1) 2-λ 0 -1

1 1-λ -1 = 0

-1 0 2-λ

1- λ -1 1 1- λ

(2- λ) -1 = 0

0 2- λ -1 0

(2- λ)2(1- λ-(1- λ) = 0

(1- λ)(2- λ)2-1 = 0

λ₁ = 1

λ₂ = 1

λ₃ = 3

λ₁ = λ₂ = 1, m = 2

λ₃ = 3, m = 1

(2- λ)x₁-x₃ = 0

x₁+(1- λ)x₂-x₃ = 0

-x₁+(2- λ)x₃ = 0

x₁-x₃ = 0

x₁-x₃ = 0

-x₁+x₃ = 0

rgA = 1

dimV = n-rgA = 3-1 = 2

Це вказує на те, що існує 2 лінійно незалежних власних вектора, що відповідають власному значенню λ₁ = 1.

Нехай x₃ = x₃

x₂ = x₂

x₁ = x₃

Тобто фундаментальна система розв’язків має вид:

x₁ 0 x₁ 1

x₂ = 1 = E₁ x₂ = 0 =E₂

x₃ 0 x₃ 1

Відповідні лінійні власні вектори мають координати:

x^λ1 = x⁽¹⁾ = (0, 1, 0)

x^λ2 = x⁽²⁾ = (1, 0, 1)

А вся сукупність складається з комбінації:

X(λ₁) = C₁x⁽¹⁾+C₂x⁽²⁾ = C₁(0, 0, 0)+C₂(1, 0, 1)

-x₁-x₃ = 0 -1 0 -1 -1 0 -1

x₁-2x₂-x₃ = 0 1 2 -1 0 2 -2

-x₁-x₃ = 0 -1 0 -1 0 0 0

rgA = 2

dimV = 3-2 = 1

Маємо 1 параметр і існує 1 лінійно незалежний вектор.

x₁+x₃ = 0 x₁ = -x₃

x₂-x₃ = 0 x₂ = x₃

x₃ = x₃ x₃ = x₃

Фундаментальна система розв’язків:

E₁ = -1

а власний вектор x^λ3 = C(-1, 1, 1) C ≠ 0

Теорема. У всякому комплексному лінійному просторі існує хоча б один власний вектор оператора А.

Приклад. У комплексному просторі знайти власні вектори, власні значення лінійного оператора А, якщо

1 -5 7

А = 1 -4 9

-4 0 5

1) |A-λE| = 0

(4-λ) -5 7 -4-λ 9 -1 9 -1 -4-λ

-1 (-4-λ) 9 =(4-λ) +5 +7

-4 0 (5-λ) 0 5-λ -4 5-λ -4 0

λ³-5x²+17λ-13 = 0

(λ-1)(x²-4 λ+13) = 0

2) λ₁ = 1

D = 6²j²

2-3j

λ_2,3 =

2+3j

Запишемо однорідну систему

(4- λ)x₁-5x₂+7x₃ = 0

x₁+(-4- λ)x₂+9x₃ = 0

-4x₁+(5- λ)x₃ = 0

3x₁-5x₂+7x₃ = 0

x₁-5x₂+9x₃ = 0

-4x₁+4x₃ = 0

3 -5 7 -1 0 1

1 -5 9 ῀ 0 -1 2

-4 0 4 0 0 0

dimV = 3-2 = 1 – незалежний вектор.

-x₁+x₃ = 0

-x₂ + 2x₃ = 0

x₁ = x₃ x₁ = 1

x₂ = 2x₃ x₂ = 2

x₃ = x₃ x₃ = 1

3) Фундаментальна система розв’язків:

E₁ = 1

xλ₁ = (1, 2, 1); xλ₁ = C(1, 2, 3)

4) λ = λ₂ = 2+3j

4-(2+3i) -5 7 2-3i -5 7

A-λ₂E = 1 -4-(2+5i) 9 = 1 -6-3i 9

-4 0 5-(2+3i) -4 0 3-3i

1 -6-3i

|A-λ₂E| = 0 => ∆₂ ≠ 0

-4 0

rg(A-λ₂E) = 2

dimV = 3-2 = 1 => існує 1 незалежний вектор

∆₂ – базисний

x₁+(-6-3i)x₂+9x₃ = 0 x₁ = x₃

=> x₂ = 5-3i

-4x₁+(3-3i)x₃ = 0 x₃ = 4

Фундаментальна система розв’язків має вид:

E₁ = 3-3i

5-3i

x^λ2 = (3-3i, 5-3i, 4)

x^λ2 = C(3-3i, 5-3i, 4)

5) λ₃ = 2-3i

x^λ3 = C(3+3i, 5+3i, 4)

Дата добавления: 2014-01-04