
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Лекция 10. На прошлой лекции мы установили, что если линия второго порядка, задана относительно ОДСК общим уравнением
|
|
|
|
На прошлой лекции мы установили, что если линия второго порядка, задана относительно ОДСК общим уравнением
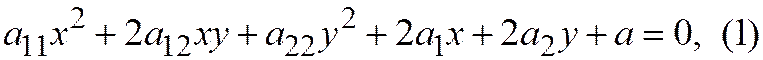 то уравнение диаметра, сопряжённого хордам неасимптотического направления
то уравнение диаметра, сопряжённого хордам неасимптотического направления 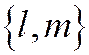 имеет вид:
имеет вид:
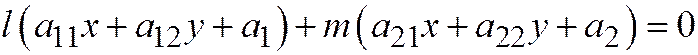 , а его направляющий вектор
, а его направляющий вектор 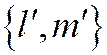 имеет координаты:
имеет координаты: 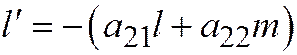 ,
, 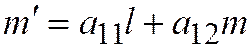 .
.
§ 147. Касательная к линии второго порядка
Пусть относительно ОДСК на плоскости задана линия второго порядка общим уравнением (1). Будем называть точку 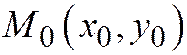 , лежащую на этой линии
, лежащую на этой линии
неособой, если среди чисел 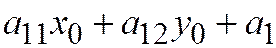 и
и 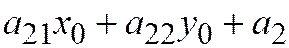 есть хотя бы одно, не равное нулю. Ясно, что точка
есть хотя бы одно, не равное нулю. Ясно, что точка 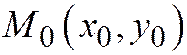 , лежащая на линии (1), является особой тогда и только тогда, она является центром линии (1).
, лежащая на линии (1), является особой тогда и только тогда, она является центром линии (1).
Таким образом, среди линий эллиптического типа только линия, распадающаяся на две мнимые пересекающиеся прямые имеет особую точку (это точка их пересечения); среди линий гиперболического типа особую точку имеет пара пересекающихся прямых (это также точка их пересечения) и, наконец, среди линий параболического типа особые точки имеет пара совпадающих прямых (особыми точками являются все точки прямой, с которой совпадают рассматриваемые прямые).
Определение. Касательной к линии второго порядка в неособой точке, лежащей на этой линии, называется прямая, проходящая через эту точку, пересекающая данную линию в двукратной точке, или совпадающая с прямой, входящей в состав данной линии.
Теорема 1. Пусть 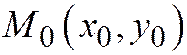 - неособая точка линии второго порядка, заданной относительно ОДСК общим уравнением (1). Тогда уравнение касательной к этой линии в точке
- неособая точка линии второго порядка, заданной относительно ОДСК общим уравнением (1). Тогда уравнение касательной к этой линии в точке 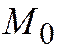 имеет вид:
имеет вид:
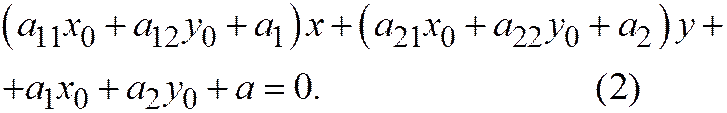 Доказательство. Рассмотрим уравнение прямой
Доказательство. Рассмотрим уравнение прямой
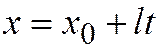 ,
, 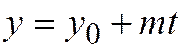 ,
,
проходящей через данную неособую точку М 0 линии (1). Подставляя в уравнение (1) 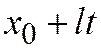 ,
, 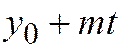 вместо
вместо 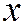 и
и 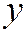 , получим:
, получим:
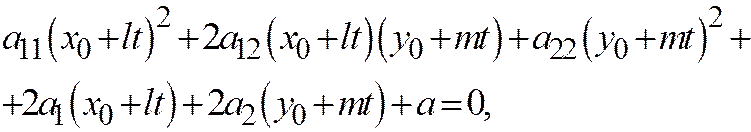
или, раскрывая скобки:
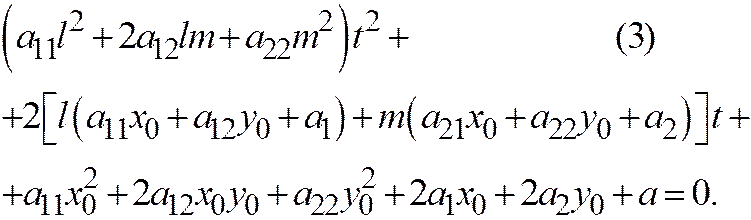
Но по предположению точка 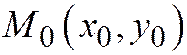 лежит на данной линии, поэтому:
лежит на данной линии, поэтому:
|
|
|
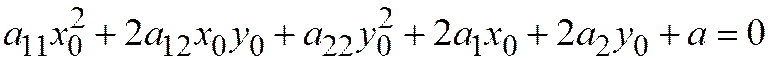 и уравнение (3) принимает вид:
и уравнение (3) принимает вид:
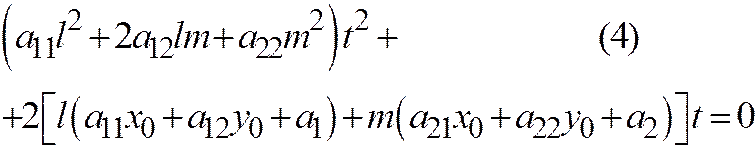
Одним из корней этого уравнения является 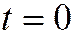 ; при этом из соотношений
; при этом из соотношений 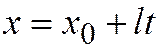 ,
, 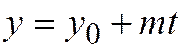 находим:
находим: 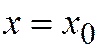 ,
, 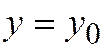 , т.е. координаты точки М 0.
, т.е. координаты точки М 0.
Для того, чтобы прямая (3) являлась касательной к линии (1), необходимо и достаточно, чтобы уравнение (4) имело и второй корень, равный нулю, а для этого необходимо и достаточно, чтобы было выполнено условие:
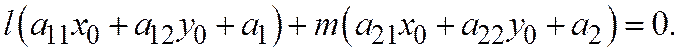 Таким образом, координаты направляющего вектора касательной будут такими:
Таким образом, координаты направляющего вектора касательной будут такими:
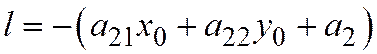 ,
, 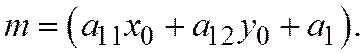 (5)
(5)
(Этот вектор ненулевой, т.к. точка 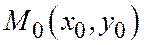 по предположению неособая (а по определению неособой точки, числа
по предположению неособая (а по определению неособой точки, числа 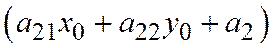 и
и 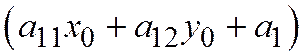 не должны одновременно обращаться в нуль).
не должны одновременно обращаться в нуль).
Если вектор 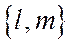 , координаты которого определяются соотношениями (5), неасимптотического направления, т.е.
, координаты которого определяются соотношениями (5), неасимптотического направления, т.е. 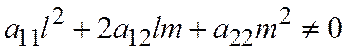 , то уравнение (4) имеет двукратный корень
, то уравнение (4) имеет двукратный корень 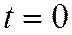 ; а если вектор
; а если вектор 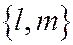 имеет асимптотическое направление, то есть
имеет асимптотическое направление, то есть 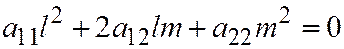 , то уравнение (4) обращается в тождество, в этом случае прямая
, то уравнение (4) обращается в тождество, в этом случае прямая 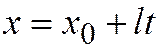 ,
, 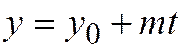 входит в состав данной линии (1) и, значит, согласно принятому определению, является касательной к линии (1) в точке
входит в состав данной линии (1) и, значит, согласно принятому определению, является касательной к линии (1) в точке 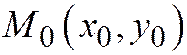 .
.
Итак, уравнения касательной к линии (1) в её неособой точке 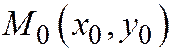 имеют вид:
имеют вид: 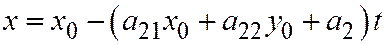 ,
, 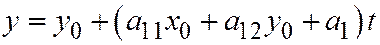 ,
,
или
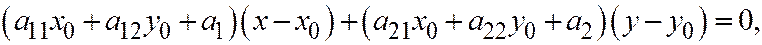 или
или
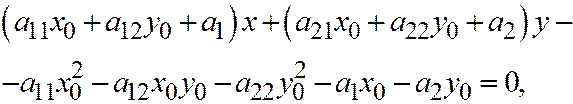
и, так как
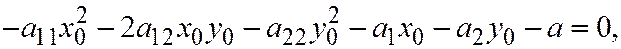
то окончательно
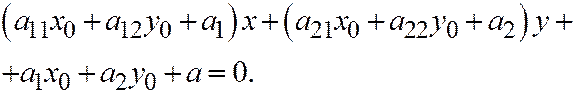 ЧТД.
ЧТД.
Теорема 2. Пусть относительно ОДСК линия второго порядка задана общим уравнением (1). Пусть диаметр 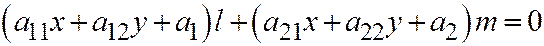 (6) этой линии, сопряженный хордам, имеющим неасимптотическое направление
(6) этой линии, сопряженный хордам, имеющим неасимптотическое направление 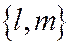 , пересекает рассматриваемую линию в неособой точке
, пересекает рассматриваемую линию в неособой точке 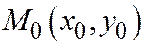 . Тогда касательная к этой линии в точке М 0 параллельна хордам, которым сопряжён диаметр (6).
. Тогда касательная к этой линии в точке М 0 параллельна хордам, которым сопряжён диаметр (6).
Доказательство. Так как диаметр (6) проходит через точку 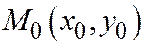 , то:
, то:
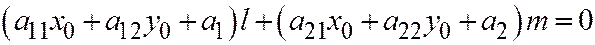 и так как
и так как 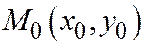 неособая точка рассматриваемой линии, то можно считать, что:
неособая точка рассматриваемой линии, то можно считать, что:
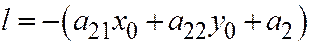 ,
, 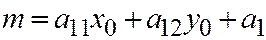 ,
,
а это координаты направляющего вектора касательной к рассматриваемой линии второго порядка в неособой точке (смотрите выше формулы (5)). ЧТД.
Замечание. Данное в этом параграфе определение касательной к линии второго порядка в её неособой точке 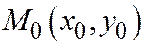 совпадает с определением касательной линии, которое даётся в курсе математического анализа. Здесь линия задана уравнением вида
совпадает с определением касательной линии, которое даётся в курсе математического анализа. Здесь линия задана уравнением вида 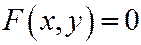 . Функция
. Функция 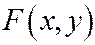 при
при 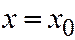 ,
, 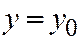 обращается в нуль, а частные производные от неё по
обращается в нуль, а частные производные от неё по 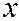 и
и 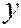 , т.е.
, т.е. 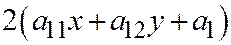 и
и 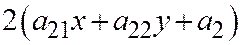 , согласно условию теоремы 1 одновременно в нуль не обращаются. Функция
, согласно условию теоремы 1 одновременно в нуль не обращаются. Функция 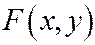 двух переменных от
двух переменных от 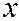 и
и 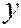 , значит уравнение касательной к линии можно записать в виде (как известно из курса матанализа):
, значит уравнение касательной к линии можно записать в виде (как известно из курса матанализа):
|
|
|
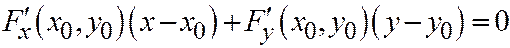 . В нашем случае:
. В нашем случае:
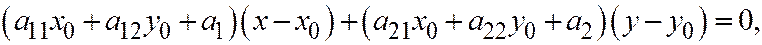 что совпадает с выведенным выше уравнением.
что совпадает с выведенным выше уравнением.
§ 148. Уравнение линии второго порядка, отнесённой к двум её сопряжённым диаметрам; уравнение линии второго порядка, отнесённой к касательной и сопряжённому к ней диаметру.
Теорема 3. Пусть относительно ОДСК линия вто-рого порядка задана общим уравнением (1). Для того, чтобы одна из осей имела направление, сопряженного хордам, параллельным другой оси, необходимо и достаточно, чтобы 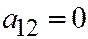 , т.е. чтобы уравнение (1) имело вид:
, т.е. чтобы уравнение (1) имело вид: 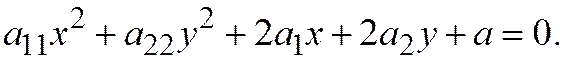
Доказательство. Пусть, например, ось  не имеет асимптотического направления. Тогда координаты вектора, параллельного диаметру, сопряжённому хордам, параллельным оси
не имеет асимптотического направления. Тогда координаты вектора, параллельного диаметру, сопряжённому хордам, параллельным оси  , будут
, будут 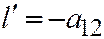 ;
; 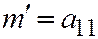 (поскольку, как известно:
(поскольку, как известно: 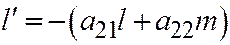 ;
; 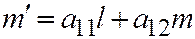 ). Но вектор
). Но вектор 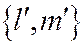 коллинеарен оси
коллинеарен оси 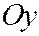 тогда и только тогда, когда
тогда и только тогда, когда 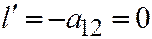 . ЧТД.
. ЧТД.
Теорема 4. Пусть относительно ОДСК линия вто-рого порядка задана общим уравнением (1) и пусть она имеет единственный центр. Тогда, если оси координат являются сопряжёнными диаметрам этой линии, а начало координат – её центром, то уравнение линии имеет вид: 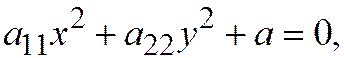 где
где
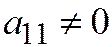 и
и 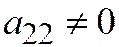 . Обратно, если уравнение линии, имеющей единственный центр, имеет относительно ОДСК уравнение
. Обратно, если уравнение линии, имеющей единственный центр, имеет относительно ОДСК уравнение 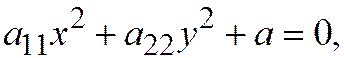 где
где 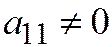 и
и 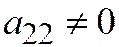 , то начало координат является центром линии, а оси координат её сопряжёнными диаметрами.
, то начало координат является центром линии, а оси координат её сопряжёнными диаметрами.
Доказательство. Если оси координат являются сопряженными диаметрами линии (1), то 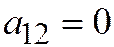 (теорема 3 этого параграфа). А так как начало координат является центром линии, то в её уравнении должны отсутствовать слагаемые с
(теорема 3 этого параграфа). А так как начало координат является центром линии, то в её уравнении должны отсутствовать слагаемые с 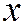 и
и 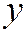 в первых степенях.
в первых степенях.
Обратно, если уравнение линии второго порядка, заданное относительно ОДСК, имеет вид: 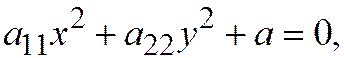 то начало координат являет-ся центром линии (что известно из теоремы 1, § 144).
то начало координат являет-ся центром линии (что известно из теоремы 1, § 144).
Далее, линия имеет единственный центр, значит 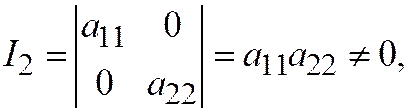 откуда
откуда 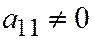 и
и 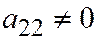 ;
;
Наконец, так как в уравнении 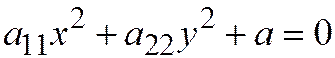
коэффициент при 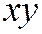 равен нулю, то оси координат являются сопряжёнными диаметрами этой линии (теорема 3 настоящей лекции, достаточность). ЧТД.
равен нулю, то оси координат являются сопряжёнными диаметрами этой линии (теорема 3 настоящей лекции, достаточность). ЧТД.
Теорема 5(1). Если ОДСК по отношению к эллипсу расположена так, что:
|
|
|
А) Оси координат являются сопряжёнными диаметрами эллипса;
Б) Единичной точкой оси 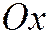 является любая точка пересечения одного из диаметров с эллипсом;
является любая точка пересечения одного из диаметров с эллипсом;
В) Единичной точкой оси 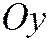 является любая точка пересечения другого диаметра с эллипсом, то уравнение эллипса будет иметь вид:
является любая точка пересечения другого диаметра с эллипсом, то уравнение эллипса будет иметь вид: 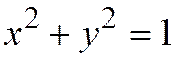 .
.
Обратно, если относительно некоторой ОДСК дано уравнение 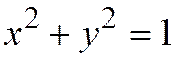 , то это уравнение эллипса, а система координат по отношению к нему обладает свойствами А), Б), В).
, то это уравнение эллипса, а система координат по отношению к нему обладает свойствами А), Б), В).
Теорема 5(2). Если ОДСК по отношению к гипер-боле расположена так, что:
Г) Оси координат являются сопряжёнными диаметрами гиперболы;
Д) Единичной точкой Е системы координат является точка пересечения любой из асимптот гиперболы с касательной в любой из точек пересечения одного из этих диаметров с гиперболой, то уравнение гиперболы будет иметь вид: 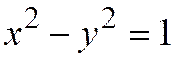 .
.
Обратно, если относительно некоторой ОДСК задано уравнение 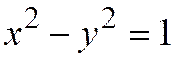 , то это уравнение гиперболы, а система координат по отношению к ней обладает свойствами Г), Д).
, то это уравнение гиперболы, а система координат по отношению к ней обладает свойствами Г), Д).
Теорема 5(3). Если ОДСК по отношению к пара-боле расположена так, что:
Е) Осью  является касательная к параболе в любой точке
является касательная к параболе в любой точке  , лежащей на этой параболе;
, лежащей на этой параболе;
Ж) Осью  является диаметром параболы, проходящий через точку
является диаметром параболы, проходящий через точку  ;
;
З) Единичная точка Е системы координат лежит на параболе, то уравнение параболы будет иметь вид: 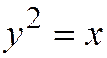 .
.
Обратно, если относительно некоторой ОДСК задано уравнение 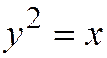 , то это уравнение параболы, а система координат по отношению к ней обладает свойствами Е), Ж),З).
, то это уравнение параболы, а система координат по отношению к ней обладает свойствами Е), Ж),З).
Доказательство 5(1). Так как оси координат являются сопряжёнными диаметрами эллипса, то его уравнение имеет вид 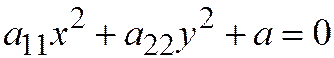 (теорема 1 сегодняшней лекции). Так как точки
(теорема 1 сегодняшней лекции). Так как точки 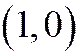 и
и 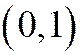 принадлежат эллипсу, то, подставляя их координаты в уравнение
принадлежат эллипсу, то, подставляя их координаты в уравнение 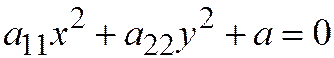 , получим выражения:
, получим выражения: 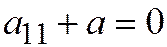 ,
, 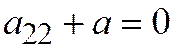 и последнее уравнение примет вид:
и последнее уравнение примет вид: 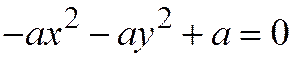 или
или 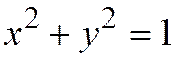 .
.
Обратно, линия 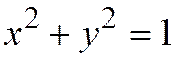 имеет единственный центр (т.к.
имеет единственный центр (т.к. 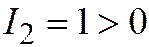 ). Далее, на основании теоремы 4 для линии, заданной уравнением
). Далее, на основании теоремы 4 для линии, заданной уравнением 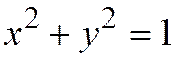 оси координат являются сопряжёнными диаметрами линии (т.к. нет слагаемого с
оси координат являются сопряжёнными диаметрами линии (т.к. нет слагаемого с 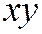 ) и оси координат пересекают линию в 4 точках:
) и оси координат пересекают линию в 4 точках: 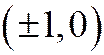 ,
, 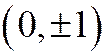 . Но этим свойством по отношению к сопряжённым диаметрам обладает только эллипс. Утверждение 5(1) доказано.
. Но этим свойством по отношению к сопряжённым диаметрам обладает только эллипс. Утверждение 5(1) доказано.
|
|
|
Доказательство 5(2). Так как оси координат являются сопряжёнными диаметрами гиперболы, то её уравнение имеет вид: 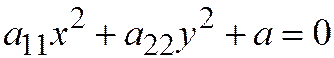 . Точка
. Точка 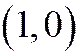 должна лежать на этой гиперболе, а точка
должна лежать на этой гиперболе, а точка 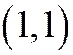 на одной из её асимптот
на одной из её асимптот 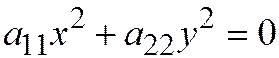 . Значит
. Значит 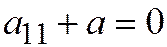 ;
; 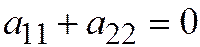 и уравнение гиперболы принимает вид:
и уравнение гиперболы принимает вид: 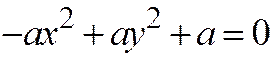 , или
, или 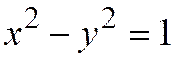 .
.
Обратно, линия 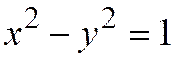 имеет единственный центр, а на основании теоремы 4, оси координат являются её сопряжёнными диаметрами. Один из этих диаметров (ось
имеет единственный центр, а на основании теоремы 4, оси координат являются её сопряжёнными диаметрами. Один из этих диаметров (ось 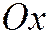 ) пересекает линию в двух точках
) пересекает линию в двух точках 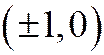 , а другой (ось
, а другой (ось 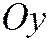 ) её не пересекает. Этим свойством по отношению к сопряжённым диаметрам обладает только гипербола. Далее, точка
) её не пересекает. Этим свойством по отношению к сопряжённым диаметрам обладает только гипербола. Далее, точка 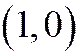 лежит на гиперболе
лежит на гиперболе 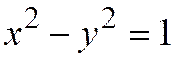 , а точка
, а точка 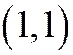 - на её асимптоте
- на её асимптоте 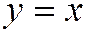 . Утверждение 5(2) доказано.
. Утверждение 5(2) доказано.
Доказательство 5(3). Диаметр параболы имеет направление, сопряжённое по отношению касательной к параболе в той точке, в которой он пересекает эту параболу, поэтому в общем уравнении параболы должно быть 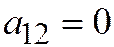 . Так как, кроме того, начало координат
. Так как, кроме того, начало координат 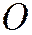 лежит на параболе, то
лежит на параболе, то 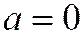 . Значит, уравнение параболы имеет вид:
. Значит, уравнение параболы имеет вид: 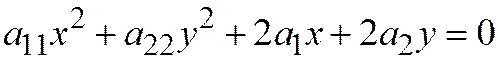 .
.
Уравнение касательной к этой параболе согласно формулы: 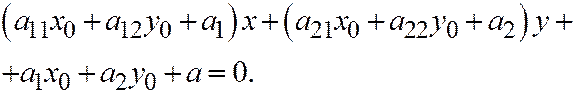 имеет вид:
имеет вид: 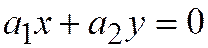 (Это потому, что начало координат
(Это потому, что начало координат 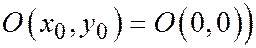 , а, т.к. касательная в начале координат является осью
, а, т.к. касательная в начале координат является осью 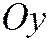 , то это уравнение эквивалентно уравнению
, то это уравнение эквивалентно уравнению 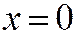 , значит
, значит 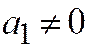 ,
, 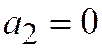 ; и последнее уравнение принимает вид:.
; и последнее уравнение принимает вид:. 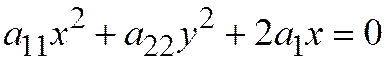 , где
, где 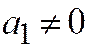 . Здесь, также
. Здесь, также 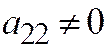 , так как в противном случае уравнение определяло бы две прямые:
, так как в противном случае уравнение определяло бы две прямые: 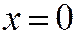 и
и 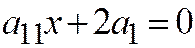 . Если бы ещё было
. Если бы ещё было 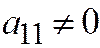 , то линия имела бы центр (притом единственный), а парабола центра не имеет. Значит
, то линия имела бы центр (притом единственный), а парабола центра не имеет. Значит 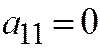 и уравнение параболы принимает вид:
и уравнение параболы принимает вид: 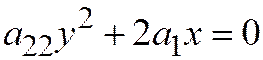 . Далее, так как единичная точка лежит на этой параболе, то
. Далее, так как единичная точка лежит на этой параболе, то 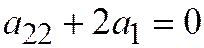 . Отсюда
. Отсюда 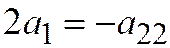 и последнее уравнение принимает вид:
и последнее уравнение принимает вид: 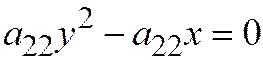 , или
, или 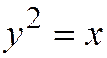 .
.
Обратно. Все диаметры линии 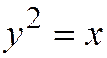 параллельны оси
параллельны оси  . В самом деле, координаты векторов, имеющих асимптотическое относительно линии
. В самом деле, координаты векторов, имеющих асимптотическое относительно линии 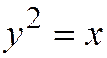 , определяются из уравнения
, определяются из уравнения 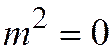 , т.е. ось
, т.е. ось  имеет асимптотическое направление.
имеет асимптотическое направление.
Пусть 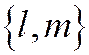 ,
, 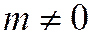 - любой вектор, не имеющий асимптотического направления относительно линии
- любой вектор, не имеющий асимптотического направления относительно линии 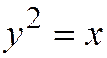 . Уравнение диаметра ему сопряжённого (согласно формуле для диаметра линии второго порядка
. Уравнение диаметра ему сопряжённого (согласно формуле для диаметра линии второго порядка 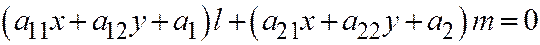 , а в нашем случае
, а в нашем случае 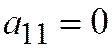 ,
, 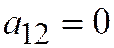 ,
, 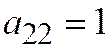 ,
, 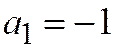 ,
, 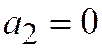 ,
, 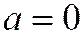 ), примет вид:
), примет вид: 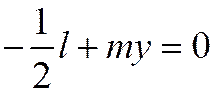 , или
, или 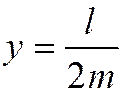 , т.е. все диаметры линии
, т.е. все диаметры линии 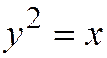 оказались
оказались
параллельными между собой, а этим свойством обладает только парабола. Далее, уравнение касательной к линии 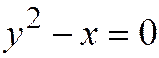 в точке
в точке 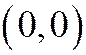 имеет вид
имеет вид 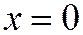 - это ось
- это ось  .
.
Уравнение диаметра, сопряжённого хордам, параллельным вектору 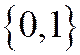 , имеет вид
, имеет вид 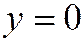 - это ось
- это ось  . Наконец, единичная точка
. Наконец, единичная точка 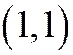 , очевидно, лежит на линии
, очевидно, лежит на линии 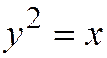 . Теорема 5 доказана.
. Теорема 5 доказана.
Теорема 6. Если неособую точку линии второго порядка принять за начало координат, за ось 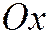 - диаметр, проходящий через эту точку, а за ось
- диаметр, проходящий через эту точку, а за ось 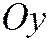 - касательную к линии второго порядка в этой точке, то уравнение линии примет вид:
- касательную к линии второго порядка в этой точке, то уравнение линии примет вид: 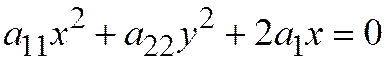 , где
, где 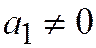 ;
; 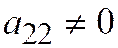 . И обратно, всякое такое уравнение в случае
. И обратно, всякое такое уравнение в случае 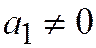 ,
, 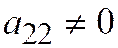 является уравнением линии второго порядка, по отношению к которой система координат обладает сформулированными выше свойствами.
является уравнением линии второго порядка, по отношению к которой система координат обладает сформулированными выше свойствами.
Доказательство. Так как касательная к линии второго порядка в её неособой точке имеет направление, которому сопряжён диаметр, проходящий через эту точку, то в общем уравнении линии коэффициент при 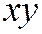 будет равен нулю. Далее, т.к. линия проходит через начало координат, то
будет равен нулю. Далее, т.к. линия проходит через начало координат, то 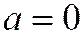 .
.
Затем, поскольку уравнение линии имеет вид: 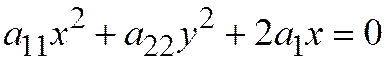 , то уравнение касательной к этой линии в начале координат будет выглядеть следующим образом:
, то уравнение касательной к этой линии в начале координат будет выглядеть следующим образом: 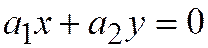 и, так как оно должно быть эквивалентно уравнению
и, так как оно должно быть эквивалентно уравнению 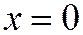 оси
оси 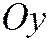 , то
, то 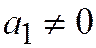 ,
, 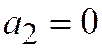 , и последнее уравнение примет вид:
, и последнее уравнение примет вид: 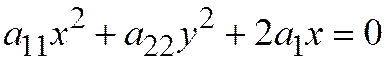 .
.
Обратно, если 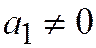 , то начало координат - неособая точка линии. Уравнение касательной к этой линии в точке
, то начало координат - неособая точка линии. Уравнение касательной к этой линии в точке 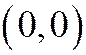 имеет вид:
имеет вид: 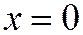 - ось
- ось 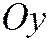 . Диаметр, сопряжённый хордам, параллельным вектору
. Диаметр, сопряжённый хордам, параллельным вектору 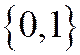 (не имеющему асимптотического направления в силу
(не имеющему асимптотического направления в силу 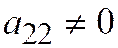 ), имеет уравнение
), имеет уравнение 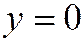 - ось
- ось  . ЧТД
. ЧТД
Теперь, давайте вместо одной линии второго порядка, заданной общим уравнением (1)
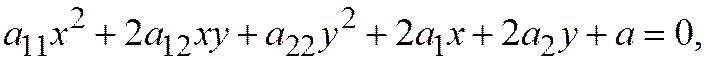 то есть уравнением
то есть уравнением 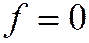 (где через
(где через 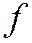 обозначена левая часть уравнения (1)), рассмотрим семейство линий
обозначена левая часть уравнения (1)), рассмотрим семейство линий 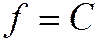 , где
, где 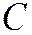 - принимает все действительные значения.
- принимает все действительные значения.
Если уравнение 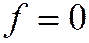 есть уравнение или действительного эллипса, или мнимого эллипса, или уравнение двух мнимых пересекающихся прямых, то в семейство
есть уравнение или действительного эллипса, или мнимого эллипса, или уравнение двух мнимых пересекающихся прямых, то в семейство 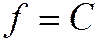 включаются все эллипсы с общим центром (т.к. координаты центра определяются из системы:
включаются все эллипсы с общим центром (т.к. координаты центра определяются из системы: 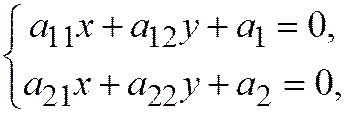 т.е. из системы уравнений не содержащих свободного члена
т.е. из системы уравнений не содержащих свободного члена 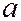 уравнения линии второго порядка (1)) и гомотетичные друг другу, причём центром гомотетии является их общий центр. В самом деле, после переноса начала координат в центр линии получим вместо уравнения
уравнения линии второго порядка (1)) и гомотетичные друг другу, причём центром гомотетии является их общий центр. В самом деле, после переноса начала координат в центр линии получим вместо уравнения 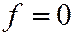 уравнение:
уравнение: 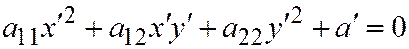 , а вместо уравнения
, а вместо уравнения 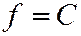 - получим уравнение:
- получим уравнение: 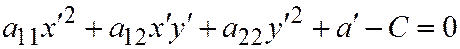 . Теперь, если
. Теперь, если 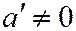 и
и 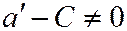 , то одно из этих уравнений переходит в другое заменой
, то одно из этих уравнений переходит в другое заменой 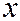 и
и 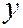 на
на 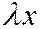 и
и 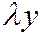 (при подходящем выборе
(при подходящем выборе 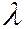 . На рис. 219 изображено семейство действительных эллипсов, входящих в семейство линий второго порядка
. На рис. 219 изображено семейство действительных эллипсов, входящих в семейство линий второго порядка 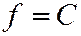 эллиптического типа.
эллиптического типа.
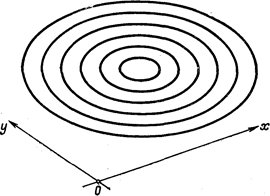
Рис. 219.
Если линия 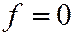 гиперболического типа, то семейство
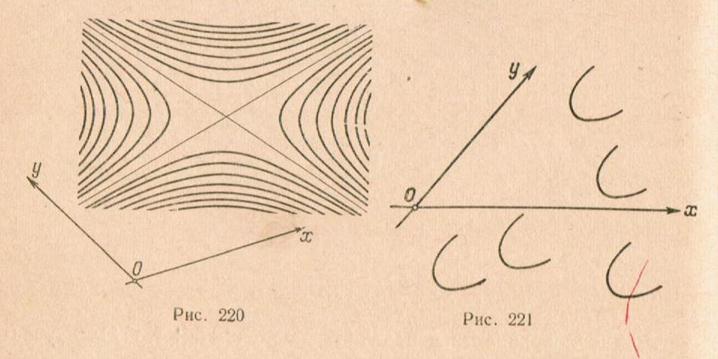
гиперболического типа, то семейство 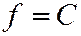 будет состоять из всех соасимптотических гипербол, при этом гиперболы, лежащие в одной и той же паре вертикальных углов, образованных их общими асимптотами, гомотетичны друг другу относительно центра (См. рис. 220)
будет состоять из всех соасимптотических гипербол, при этом гиперболы, лежащие в одной и той же паре вертикальных углов, образованных их общими асимптотами, гомотетичны друг другу относительно центра (См. рис. 220)
Если линия 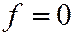 - уравнение параболы, то
- уравнение параболы, то 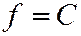 есть уравнения парабол, полученных параллельным переносом (См. рис. 221)
есть уравнения парабол, полученных параллельным переносом (См. рис. 221)
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 346; Нарушение авторских прав?; Мы поможем в написании вашей работы!