Основные метрические задачи, связанные с плоскостью

Плоскость в прямоугольной системе координат

Лекция 12

1. Уравнение плоскости, заданной точкой и вектором нормали.

Ненулевой вектор называется перпендикулярным плоскости, если он ортогонален любому вектору, параллельному этой плоскости или лежащему в ней.

Вектор, перпендикулярный плоскости, называется вектором нормали этой плоскости или ее нормальным вектором.

Вектор нормали плоскости 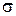будем обозначать через .

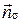Пусть в пространстве дана прямоугольная декартова система координат 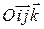, плоскость 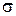, 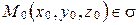и .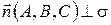

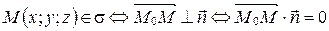(рис. 70).

Переходя к координатам, получаем уравнение

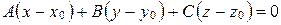. (27)

Уравнение (27) называется уравнением плоскости, заданной точкой и вектором нормали.

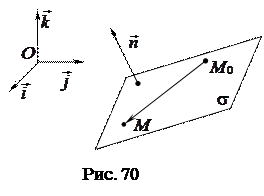Следовательно, коэффициенты А, В и С при х, у и z в общем уравнении плоскости, заданном в прямоугольной декартовой системе координат, имеют следующий геометрический смысл: А, В и С есть координаты вектора нормали данной плоскости.

2. Расстояние от точки до плоскости.

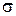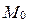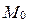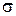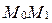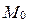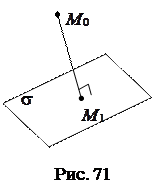
Пусть в пространстве дана плоскость и не принадлежащая ей точка . Расстоянием от точки до плоскости называется длина перпендикуляра , проведенного из точки к плоскости 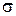(рис. 71): 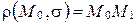. Если , то .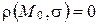

Пусть в прямоугольной декартовой системе координат 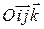дано уравнение плоскости 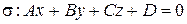и точка 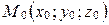, не принадлежащая плоскости 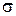. Тогда расстояние от точки 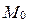до плоскости 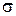вычисляется по формуле:

.

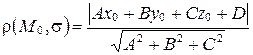Доказательство этой формулы аналогично доказательству формулы для вычисления расстояния от точки до прямой на плоскости.

3. Расстояние между двумя параллельными плоскостями.

Пусть две параллельные плоскости и 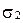заданы в прямоугольной декартовой системе координат 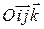уравнениям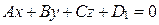и и 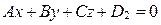соответственно. Выведем формулу для вычисления .

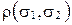Заметим, что 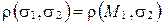, где 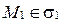. Пусть 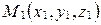. Так как 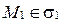, то 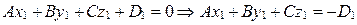. Поэтому 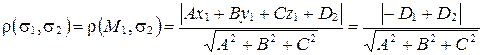. Итак,

.

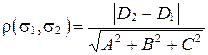4. Угол между двумя пересекающимися плоскостями.

Пусть 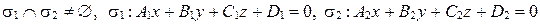в прямоугольной декартовой системе координат .

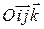Две пересекающиеся плоскости образуют четыре двугранных угла. Углом между двумя пересекающимися плоскостями будем называть тот из четырех двугранных углов, который по величине не превосходит остальные. Величину линейного угла этого двугранного угла будем обозначать через .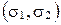

Выведем формулу для вычисления косинуса угла между плоскостями и .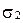

Пусть 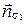и 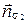- векторы нормалей плоскостей и 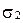. Зная величину угла 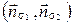, можно вычислить величину угла 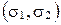. При этом возможны два случая:

а) Если 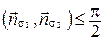(рис. 72, а), то 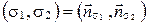, следовательно, .

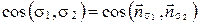б) Если 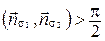(рис. 72, б), то 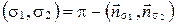, следовательно, .

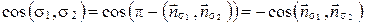Из пунктов а) и б) следует, что

.

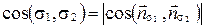Учитывая, что 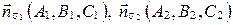, получаем:

.

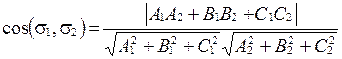Условие перпендикулярности двух плоскостей имеет вид:

.

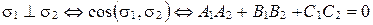Задания для самостоятельной работы

1. Можно ли в аффинной системе координат пользоваться уравнением (27) и почему?

2. Выведите уравнение плоскости, проходящей через точку 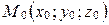и перпендикулярной каждой из плоскосте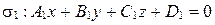й и 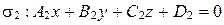, уравнения которых даны в прямоугольной системе координат.

3. Докажите, что уравнение плоскости, проходящей через точк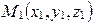и и 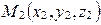перпендикулярно к плоскости 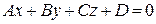, может быть представлено в следующем виде:

.

4. Пользуясь уравнением (27), найдите уравнения координатных плоскосте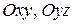й и 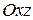прямоугольной декартовой системы координат .

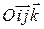5. Найдите объем куба, одна грань которого принадлежит координатной плоскости 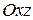, а другая – плоскости .

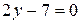6. Вычислите косинусы углов, которые образует с координатными плоскостями прямоугольной декартовой системы координат плоскость .

Дата добавления: 2014-01-04