Свойства гиперболы

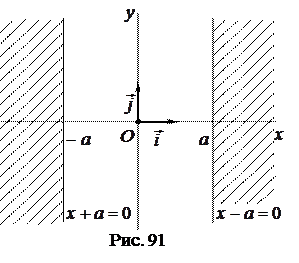1°. Из уравнения (40) следует, что 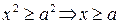или 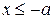. Следовательно, все точки гиперболы лежат вне полосы, ограниченной прямыми и (рис. 91).

2°. Симметрия относительно начала координат и осей координат.

Пусть 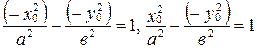и . Из первого тождества следует, что 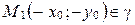, из второго – что 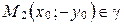, из третьего – что , а это означает, что гипербола 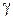симметрична относительно начала координат, оси и оси соответственно. Таким образом, точка 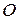является центром симметрии, оси и - осями симметрии гиперболы .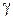

Прямая, проходящая через фокусы, называется действительной осью симметрии, а перпендикулярная к ней ось – мнимой осью симметрии гиперболы.

3°. Точки пересечения гиперболы с осями симметрии.

Чтобы найти точки пересечения гиперболы 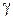с осью , надо решить систему их уравнений:

Решая систему, получаем: .

Аналогично находим, что .

Точки пересечения гиперболы со своими осями симметрии называются вершинами гиперболы. Таким образом, гипербола имеет две вершины.

Отрезки 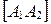и называются соответственно действительной и мнимой «осями» гиперболы, а положительные числа и 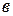- действительной и мнимой «полуосями» гиперболы.

4°. Найдем точки пересечения гиперболы с прямой .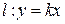

Для этого решим систему

Получаем уравнение 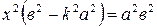. Корни 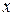- это абсциссы точки пересечения прямой 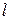с 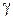. Рассмотрим три случая:

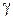1) Если , т.е. , то и 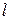имеют две общие точки;

2) Если 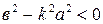, т.е. , то ;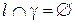

3) Если 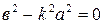, т.е. 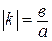, то .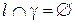

Следовательно, все точки гиперболы расположены в заштрихованных областях (рис. 92). Гипербола имеет две ветви.

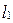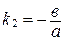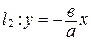Случаю 3) соответствуют две прямые и с угловыми коэффициентами и . Эти прямые (и ) называются асимптотами гиперболы.

При неограниченном возрастании абсолютной величины абсциссы точки 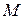гиперболы точка неограниченно приближается к асимптоте.

Учитывая свойства 1°- 4°, построим изображение гиперболы (рис. 93):

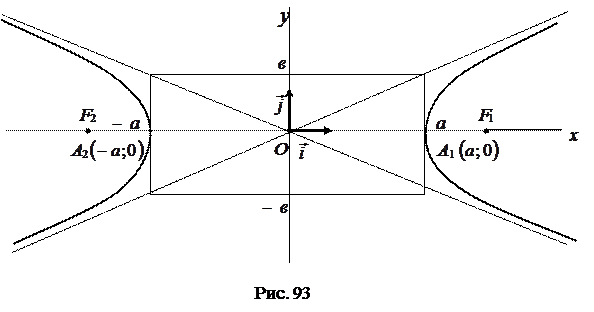Число 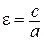называется эксцентриситетом гиперболы. Так как для гиперболы , то 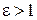. Чем больше , тем больше гипербола «вытянута» вдоль мнимой оси.

Гипербола, у которой , называется равносторонней. Ее каноническое уравнение . Уравнения ее асимптот .

Директрисами эллипса называются две прямые, параллельные мнимой оси и отстоящие от нее на расстоянии .

Уравнения директрис:

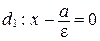или ;

или (рис. 94).

Гипербола обладает следующим директориальным свойством: для любой точки 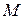, принадлежащей гиперболе, отношение расстояния от 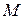до фокуса к расстоянию от 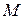до соответствующей директрисы равно эксцентриситету, т.е.

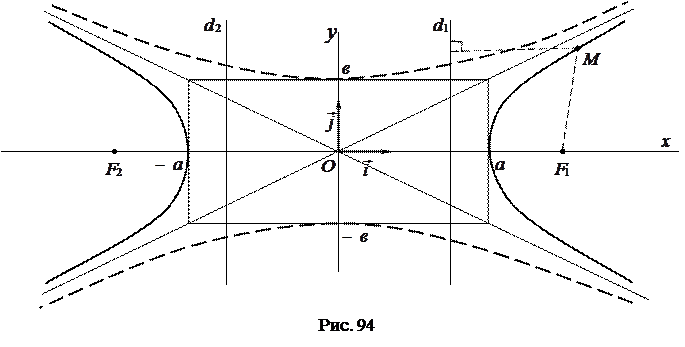
(рис. 94).

Замечание 1. Директрисы гиперболы не имеют общих точек с гиперболой.

Гипербола 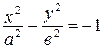называется сопряженной к гиперболе 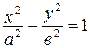. Ее мнимой осью является ось (на рис. 94 она изображена пунктиром).

Задания для самостоятельной работы

1. Приведите уравнение гиперболы к каноническому виду:

а) 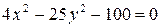;	в) ;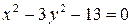
б) ;	г) .

2. Дано каноническое уравнение гиперболы. Найдите действительную и мнимую «полуоси», координаты вершин, координаты фокусов, фокальное расстояние, фокальные радиусы точки 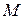, эксцентриситет, уравнения директрис:

а) ;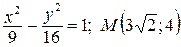

б) .

3. Постройте изображение гиперболы, ее фокусов и директрис:

а) ;

б) .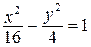

4. Докажите, что эксцентриситет равносторонней гиперболы равен .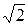

Дата добавления: 2014-01-04