
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Определение напряжений в грунтовом массиве от действия местной нагрузки на его поверхности
|
|
|
|
Общие положения. Распределение напряжений в основании в большой мере зависит от формы фундамента в плане. Поскольку в промышленном и гражданском строительстве обычно используются ленточные, прямоугольные или круглые фундаменты, основное практическое значение имеет расчет напряжений для случаев плоской, пространственной и осесимметричной задач.
Напомним, что распределение напряжений в основании определяется методами теории упругости. Основание при этом рассматривается как упругое полупространство, бесконечно простирающееся во все стороны от горизонтальной поверхности загружения. Полученные методами теории упругости напряжения соответствуют стабилизированному состоянию, т. е. такому периоду времени, когда все процессы консолидации и ползучести грунтов основания под действием приложенной нагрузки уже завершились и внешняя нагрузка оказывается полностью уравновешенной внутренними силами (эффективными напряжениями в грунте). Кроме того, принимается, что зоны развития пластических деформаций, возникающие в основании у краев фундамента (вследствие краевого эффекта), незначительны и не оказывают заметного влияния на распределение напряжений в основании.
Приведем общий ход решения задач о распределении напряжений в упругом полупространстве под действием местной нагрузки. В основе лежит решение задачи о действии вертикальной сосредоточенной силы, приложенной к поверхности упругого полупространства, полученное в 1885 г. Ж. Буссинеском. Это решение позволяет определить все компоненты напряжений и деформаций в любой точке полупространства М от действия силы Р (рис. 8.5, а). Поскольку для практических расчетов (в частности, для определения осадки фундамента) наибольшее значение имеют вертикальные сжимающие напряжения, ограничимся в качестве примера выражением для этой составляющей напряжений
|
|
|
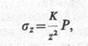 (8.8)
(8.8)
где


Рис. 8.5. Расчетные схемы основных задач: а – задача Буссинеска; б – задача о действии нескольких сил; в – задача Фламана
Теперь, используя принцип суперпозиции, легко определить значение вертикального сжимающего напряжения в точке М при действии нескольких сосредоточенных сил, приложенных на поверхности (рис. 8.5, б):
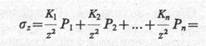
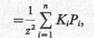 (8.9)
(8.9)
где Кi определяется по формуле (8.8) в зависимости от соотношения ri/z, причем координата z постоянна для данной точки М.
Представляет также интерес решение для вертикальной сосредоточенной силы Р в условиях плоской задачи (рис. 8.5, в), полученное Фламаном в 1892 г. в виде
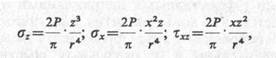 (8.10)
(8.10)
где r2=x2+z2.
Зная закон распределения нагрузки на поверхности в пределах контура загружения, можно, интегрируя выражение (8.8) в пределах этого контура, определить значения напряжений в любой точке основания для случаев осесимметричной и пространственной нагрузки, а интегрируя выражение (8.10) — для случая плоской нагрузки. Точные решения некоторых из этих задач будут приведены ниже.
Приближенные решения. Используя приведенные выражения, можно достаточно просто с некоторым приближением определить напряжения в любой точке основания при любой форме фундамента и заданном законе распределения нагрузки. Поясним это на примере пространственной задачи.
Пусть на поверхности полупространства в пределах сложного контура действует некоторая распределенная нагрузка (рис. 8.6). Разбивая контур загружения на элементарные прямоугольники, заменим в пределах каждого прямоугольника распределенную нагрузку соответствующей силой Pi = p(x, у) Δх Δy.

Рис. 8.6. Схема к приближенному расчету напряжений в любой точке основания
|
|
|
Очевидно, что для элементов, прилегающих к контуру нагрузки, размеры площадей должны быть уточнены в соответствии с сеткой разбивки. Тогда от каждой силы Р, напряжение ал в точке М, находящейся на глубине z от поверхности нагружения, определится по формуле (8.8), где r2=х2+у2. Очевидно, что для определения полного напряжения σz от действия всех элементарных сил необходимо выполнить суммирование по площади загружения.
Аналогичным образом, используя выражения (8.10), можно получить значения всех компонент напряжений для случая плоской задачи.
Точность решения зависит от размеров элементарных прямоугольников, на которые разбивается загруженный участок, и повышается с увеличением z. Если обозначить длинную сторону прямоугольника сетки разбиения Δу, то, как отмечает Н. А. Цытович, на глубине z=2Δy значение σz будет отличаться от полученного строгим решением на 6%, а на глубине z=4 Δy – ужена на 2%.

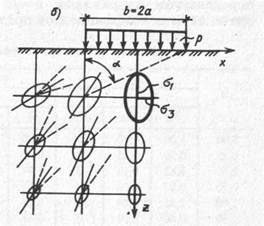
Рис. 8.7. Схема для расчета напряжений в случае плоской задачи (а); расположение эллипсов напряжений в основании (б)
Плоская задача. Действие равномерно распределенной нагрузки.
Схема для расчета напряжений в основании в случае плоской задачи при действии равномерно распределенной нагрузки интенсивностью р показана на рис. 8.7, а. Для этого случая Г. В. Колосовым получены следующие точные выражения для определения компонент напряжений в любой точке упругого полупространства:
 (8.11)
(8.11)
Если соотношения геометрических характеристик а, х, z в этих
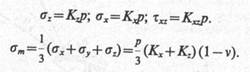 (8.12)
(8.12)
Коэффициенты влияния Кz, Кx, Кxz зависят от безразмерных параметров х/b и z/b, где х и z -координаты точки, в которой определяются напряжения, b=2а –ширина полосы загружена Значения этих коэффициентов приведены в табл. 8.1.
Таблица 8.1. Значения коэффициентов Кz, Кx, Кxz
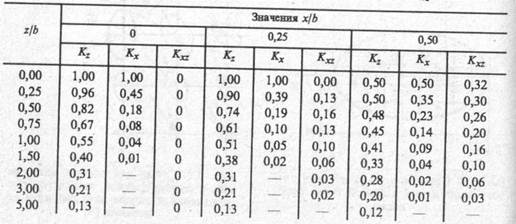
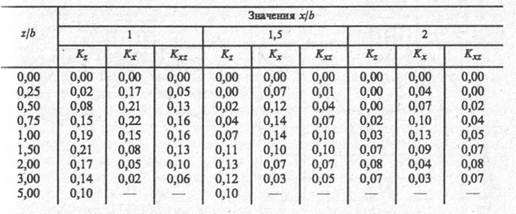

Рис. 8.8. Изолинии напряжений для случая плоской задачи и эпюра вертикальных сжимающих напряжений по оси полосы загружения
Рассчитанные таким образом величины представлены на рис. 8.8, а – в в виде линий равных напряжений (изолиний напряжений). Для напряжений σz показаны лишь изолинии слева от вертикальной оси, справа будет иметь место симметричное положение линий равных напряжений. Видно, что по мере удаления от поверхности загружения интенсивность напряжений уменьшается и стремится к нулю. Вертикальные сжимающие напряжения σz распространяются преимущественно в глубь основания, горизонтальные сжимающие напряжения σz — в стороны от полосы загружения. Касательные напряжения τxz концентрируются по преимуществу под краями загруженной полосы.
|
|
|
В расчетах осадок широко используется эпюра напряжений σz, построенная по вертикальной оси, проходящей через центр площади фундамента. Такая эпюра показана справа от оси z. Если рассечь соответствующие изолинии напряжений вертикальной или горизонтальной плоскостью, то легко построить эпюры напряжений, действующих в этих сечениях.
Аналогичные решения получены и для других видов нагрузок (например, треугольной, параболической и т д.). Соответствующие коэффициенты влияния приведены в табличной форме в различных источниках (в частности, в учебниках Н. А. Цытовича по механике грунтов). Используя эти таблицы, можно самую сложную форму нагрузки представить как комбинацию простейших эпюр, рассчитать в требуемой точке напряжения от каждой эпюры и, используя принцип суперпозиции, определить в этой точке суммарное напряжение от полной нагрузки.
В некоторых случаях при анализе напряженного состояния основания оказывается удобнее пользоваться главными напряжениями. Тогда значения главных напряжений в любой точке упругого полупространства под действием полосовой равномерно распределенной нагрузки можно определить по формулам И. X. Митчела:
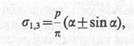 , (8.13)
, (8.13)
где α — угол видимости, образованный лучами, выходящими из данной точки к краям загруженной полосы (рис. 8.7, б). Эта формула позволяет не только определить значения главных напряжений, но и их ориентацию по отношению к осям х и z. Максимальное напряжение σ1 действует по направлению биссектрисы угла видимости в данной точке, минимальное σ3 — в перпендикулярном ему направлении. На рис. 8.7, б для иллюстрации построены эллипсы напряжений, полуоси которых соответствуют значениям и направлению главных напряжений.
|
|
|
Пространственная задача. Действие равномерно распределенной нагрузки. Условия пространственного напряженного состояния в основании возникают тогда, когда по его поверхности действует местная нагрузка, распределенная по площади квадрата, прямоугольника, круга, эллипса и т. п. В этом случае неизвестными являются все компоненты напряжений. Для ряда таких задач имеются решения, полученные в замкнутом виде.
Значения вертикальных сжимающих напряжений σz в любой точке основания от действия нагрузки интенсивностью р, равномерно распределенной по площади прямоугольника размером lxb, впервые были получены А. Лявом в 1935 г. Практический интерес представляют компоненты напряжений σzC, относящиеся к вертикали, проведенной через угловую точку С этого прямоугольника, и σz0, действующие по вертикали, проходящей через его центр (рис. 8.9).

Рис. 8.9. Сжимающие напряжения под центром и под углом прямоугольника с равномерно распределенной нагрузкой
Используя введенные выше понятия коэффициентов влияния, можно записать:
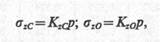 (8.14)
(8.14)
где KzC и Kz0 — соответственно коэффициенты влияния для угловых и центральных напряжений, зависящие от соотношения сторон загруженного прямоугольника и относительной глубины точки, в которой определяются напряжения.
Между значениями σzC и σz0 имеется определенное соотношение. Можно показать, что напряжения в точках, расположенных на вертикали, проходящей через центр площади загружения, равны учетверенным значениям угловых напряжений, действующих на удвоенной глубине, т. е.
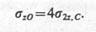 (8.15)
(8.15)
Тогда оказывается удобным выразить формулы (8.14) через общий коэффициент влияния α и записать их в виде
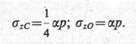 (8.16)
(8.16)
Коэффициент α зависит от безразмерных параметров m и n. Параметр n = l/b для обоих случаев является одинаковым. Следует помнить, что при определении углового напряжения σzC параметр m=z/b. при определении напряжения под центром прямоугольника σz0 параметр m=2z/b. Значения коэффициентов α приведены в табл. 8.2. Здесь же даны значения коэффициента α для определения сжимающих напряжений под центром нагрузки, равномерно распределенной по площади круга радиусом r=√π/А, причем m=2z/r.
Таблица 8.2. Значения коэффициента α.

Приведенные выражения позволяют определить сжимающие напряжения в основании не только под центром или углом прямоугольной площадки загружения, но и по вертикали, проходящей через любую точку поверхности. Для этого применяется метод угловых точек. Здесь возможны три варианта решения (рис.8.10).
Пусть вертикаль проходит через точку М, лежащую на контуре прямоугольника. Разделив этот прямоугольник на два так, чтобы точка М являлась угловой для каждого из них, можно представить напряжения σzM как сумму угловых напряжений I и II прямоугольников, т. е.
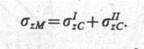 (8.17)
(8.17)

Рис. 8.10 Схема для расчета напряжений методом угловых точек
Соответственно значения напряжения σIzC и σIIzC определяются по указанным выше правилам. Коэффициенты αI и αII находятся из табл. 8.2 по значениям безразмерных параметров lI/bI, z/bI и lII/bII, z/bII, где lI, bI, lII, bII — размеры сторон соответствующих прямоугольников. При этом всегда принимается, что b≤l.
Если точка М лежит внутри контура прямоугольника, то его следует разделить на четыре части так, чтобы эта точка являлась угловой для каждого составляющего прямоугольника.
Тогда
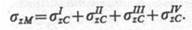 (8.18)
(8.18)
Наконец, если точка М лежит вне контура загруженного прямоугольника, то его нужно достроить так, чтобы эта точка вновь оказалась угловой. Тогда, полагая, что напряжения в точке М возникают от действия нагрузки, распределенной по площади прямоугольников I и II, необходимо вычесть напряжения от действия той же фиктивной нагрузки, распределенной по площади прямоугольников III и IV, т. е. действительное напряжение определится выражением
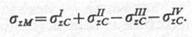 (8.19)
(8.19)
Естественно, что и в этих случаях правила определения угловых напряжений и соответствующих им значений коэффициентов α будут те же, что и приведенные для первого варианта.
Методом угловых точек обычно пользуются для расчетов взаимного влияния фундаментов, расположенных в непосредственной близости друг от друга.
Влияние формы и площади фундамента в плане. Пользуясь формулой (8.16) и данными табл. 8.2, можно построить эпюры нормальных напряжений σz по вертикальной оси, проходящей через центр прямоугольного фундамента. В качестве примера на рис. 8.11 в относительных координатах построены такие эпюры для случаев: 1 — квадратного фундамента при l=b; 2 — ленточного фундамента (l≥10b) шириной b; 3 — то же, шириной 2b. Легко заметить, что в случае пространственной задачи (кривая 1) напряжения с глубиной затухания значительно быстрее, чем для плоской задачи (кривая 2). Увеличение ширины, а следовательно, и площади фундамента (кривая 3) приводит к еще более медленному затуханию напряжений с глубиной.
Это обстоятельство легко объяснить исходя из принципа суперпозиции. Представляя, например, ленточный фундамент как ряд квадратных фундаментов, установленных вплотную друг к другу, можно с помощью метода угловых точек учесть дополнительное влияние нагрузки, действующей на соседние фундаменты.
Указанная закономерность имеет важное практическое значение. Если, например, в основании на некоторой глубине залегает слабый прослоек (ил на рис. 8.11), то можно подобрать такую форму и площадь фундамента, чтобы напряжения на кровле этого прослойка были меньше его несущей способности. В противном случае возможны чрезмерные осадки из-за выдавливания грунта слабого прослойка в стороны от оси фундамента.
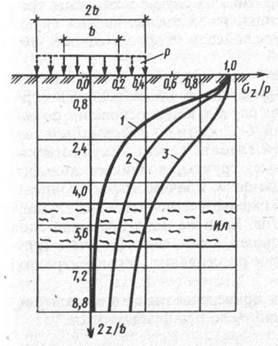
Рис. 8.11. Характер распределения напряжений по оси фундамента в зависимости от формы и площади его подошвы
Влияние неоднородности напластования грунтов. Приведенные выше решения справедливы для случая, когда основание сложено грунтами, близкими по деформационным показателям. Если же на некоторой глубине залегают существенно более жесткие (например, скальные) грунты, возникает концентрация напряжений σz по оси фундамента, причем эффект концентрации напряжений тем больше, чем меньше относительная глубина залегания кровли этого слоя грунтов. Если же подстилающий слой грунта обладает значительно большей сжимаемостью, чем несущий, напротив, отмечается некоторое рассеивание (деконцентрация) напряжений σz.
На рис. 8.12 в качестве примера приведены также в относительных координатах эпюры напряжений σz по оси фундаментов.
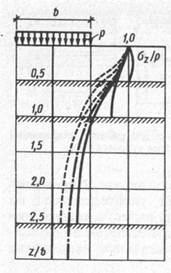
Рис. 8.12. Характер распределения напряжений σz по оси фундамента при расположении подстилающего слоя на разной глубине:
- ∙ - ∙ - относительно однородное по сжимаемости основание;
----- при наличии на соответствующих относительных глубинах z/b практически несжимаемого слоя;
- - - то же, но значительно более слабого слоя, чем несущий слой грунта
|
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 21140; Нарушение авторских прав?; Мы поможем в написании вашей работы!