Генетический алгоритм

1. Выбрать начальную популяцию I ₀ и положить
f* = max { f (i) | i 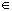I ₀}, k: = 0.

2. Пока не выполнен критерий остановки делать следующее.

2.1. Выбрать родителей i ₁, i ₂ из популяции I_k.
2.2. Построить i' по i ₁, i ₂.
2.3. Модифицировать i'.
2.4. Если f* < f (i'), то f*: = f (i').
2.5. Обновить популяцию и положить k: = k+1.

Остановимся подробнее на основных операторах этого алгоритма: селекции, скрещивании и мутации. Среди операторов селекции наиболее распространенными являются два вероятностных оператора пропорциональной и турнирной селекции. При пропорциональной селекции вероятность на k -м шаге выбрать решение i в качестве одного из родителей задается формулой

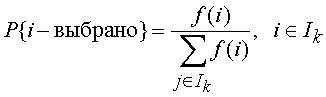
в предположении, что f (i) > 0 для всех i Î I. При турнирной селекции формируется случайное подмножество из элементов популяции и среди них выбирается один элемент с наибольшим значением целевой функции. Турнирная селекция имеет определенные преимущества перед пропорциональной, так как не теряет своей избирательности, когда в ходе эволюции все элементы популяции становятся примерно равными по значению целевой функции. Операторы селекции строятся таким образом, чтобы с ненулевой вероятностью любой элемент популяции мог бы быть выбран в качестве одного из родителей. Более того, допускается ситуация, когда оба родителя представлены одним и тем же элементом популяции.

Как только два решения выбраны, к ним применяется вероятностный оператор скрещивания (crossover). Существует много различных версий этого оператора [15], среди которых простейшим, по видимому, является однородный оператор. По решениям i ₁, i ₂ он строит решение i' присваивая каждой координате этого вектора с вероятностью0,5 соответствующее значение одного из родителей. Если вектора i ₁, i ₂ совпадали скажем по первой координате, то вектор i' "унаследует" это значение. Геометрически, оператор скрещивания случайным образом выбирает в гиперкубе вершину i', которая принадлежит минимальной грани, содержащей вершины i ₁, i ₂. Можно сказать, что оператор скрещивания старается выбрать новое решение i' где-то между i ₁, i ₂ полагаясь на удачу. Более аккуратная процедура могла бы выглядеть таким образом. Новым решением i' является оптимальное решение исходной задачи на соответствующей грани гиперкуба. Конечно, если расстояние Хемминга между i ₁, i ₂ равно n, то задача оптимального скрещивания совпадает с исходной. Тем не менее даже приближенное решение этой задачи вместо случайного выбора заметно улучшает работу генетического алгоритма [8, 9, 10, 14]. По аналогии с однородным оператором скрещивания легко предложить и другие операторы, использующие не только два, но и произвольное число решений из популяции. Например, в [20] использовалось восемь родителей. Другие примеры можно найти в [13]. С адаптацией этой идеи к задаче коммивояжера можно познакомиться в [17].

Оператор мутации, применяемый к решению i' в п. 2.3. генетического алгоритма, с заданной вероятностью p _m Î (0, 1) меняет значение каждой координаты на противоположное. Например, вероятность того, что i' = (0, 0, 0, 0, 0) в ходе мутации перейдет в j' = (1, 1, 1, 0, 0), равна p_m ´ p_m ´ p_m ´ (1 – p_m) ´ (1 – p_m) > 0. Таким образом, с ненулевой вероятностью решение i' может перейти в любое другое решение. Отметим, что модификация решения i' может состоять не только в случайной мутации, но и в частичной перестройке решения алгоритмами локального поиска. Применение локального спуска позволяет генетическому алгоритму сосредоточиться только на локальных оптимумах. Множество локальных оптимумов может оказаться экспоненциально большим и на первый взгляд кажется, что такой вариант алгоритма не будет иметь больших преимуществ. Однако экспериментальные исследования распределения локальных оптимумов свидетельствуют о высокой концентрации их в непосредственной близости от глобального оптимума [11, 18]. Это наблюдение известно как гипотеза о существовании "большой долины" для задач на минимум или "центрального горного массива" для задач на максимум.

Гипотеза 1.
В среднем локальные оптимумы расположены гораздо ближе к глобальному оптимуму чем к случайно выбранной точке. Их распределение в области допустимых решений на является равномерным. Они концентрируются в районе глобального оптимума, занимая область небольшого диаметра.

Эта гипотеза отчасти объясняет работоспособность генетических алгоритмов. Если в популяции собираются локальные оптимумы, которые согласно гипотезе сконцентрированы в одном месте, и очередное решение i' выбирается где-то между двумя произвольными локальными оптимумами, то такой процесс имеет много шансов найти глобальный оптимум. Аналогичные рассуждения объясняют работоспособность и других локальных алгоритмов. В связи с этим проверка и теоретическое обоснование данной гипотезы представляет несомненный интерес.

45. Нейронный слой Кохонена. Кластеризация.

http://ru.wikipedia.org/wiki/%D0%9D%D0%B5%D0%B9%D1%80%D0%BE%D0%BD%D0%BD%D0%B0%D1%8F_%D1%81%D0%B5%D1%82%D1%8C_%D0%9A%D0%BE%D1%85%D0%BE%D0%BD%D0%B5%D0%BD%D0%B0

http://habrahabr.ru/post/143668/

http://mechanoid.kiev.ua/neural-net-kohonen-clusterization.html

Дата добавления: 2014-01-04