Теорема 2 (Пуансо)

При сферическом движении подвижный аксоид катится по неподвижному без проскальзывания; при этом в каждый момент времени подвижный и неподвижный аксоиды касаются друг друга в точках мгновенной оси вращения.

3º. Скорости точек твердого тела
при сферическом движении

Скорости точек твердого тела определяются по формуле Эйлера

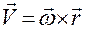. (3.13.7)

Эта формула имеет тот же вид, что и для скорости точек твердого тела, вращающегося вокруг неподвижной оси.

Однако существенным отличием ее применения для определения скоростей являются следующие свойства указанных движений:

· при вращении вокруг неподвижной оси — вектор 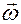при всех коллинеарен оси вращения, которая не изменяет свою ориентацию в абсолютном пространстве,

· при сферическом движении — вектор 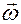коллинеарен мгновенной оси вращения, но эта ось может изменять свою ориентацию в абсолютном пространстве.

Поэтому при сферическом движении, как и при вращении вокруг неподвижной оси, каждая точка твердого тела имеет мгновенную скорость, совпадающую по величине с ее круговой скоростью, т.е. со скоростью, которую она имела бы при круговом движении, совершаемом ею при вращении вокруг оси, совпадающей с мгновенной осью вращения.

Угловая скорость кругового движения при таком вращении совпадает с вектором .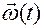

Однако в отличие от вращения вокруг неподвижной оси, на сферическом движении плоскость кругового движения точки при изменении не будет занимать неизменное положение в абсолютном пространстве.

Она будет менять свою ориентацию в нем вместе с изменением ориентации мгновенной оси вращения, и менять свое положение в пространстве вместе с этой осью и материальной точкой.

Из формулы (3.13.7)

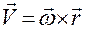(3.13.7)

следует, что при решении практических задач, связанных с построением скоростей точек твердого тела, можно поступить следующим образом:

· определить вектор ;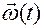

· затем построить мгновенную ось вращения.

Она проходит через неподвижную точку 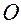и коллинеарна вектору .

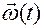Далее, для построения мгновенных скоростей точек твердого тела применять все те приемы, которые разработаны для твердого тела, вращающегося вокруг неподвижной оси, считая, что неподвижной является построенная мгновенная ось вращения.

4º. Ускорения точек твердого тела
при сферическом движении

Ускорение любой точки твердого тела определяется по формуле Ривальса. На сферическом движении эта формула принимает вид:

,

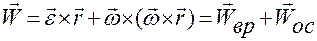где

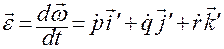— вектор мгновенного углового
ускорения,

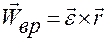— вращательное ускорение точки
твердого тела,

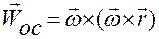— осестремительное ускорение точки
твердого тела.

Положим 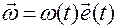, где 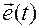— орт мгновенной оси вращения. Тогда вектор углового ускорения можем представить в следующей форме

.

Обозначим

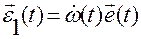· — угловое ускорение вокруг мгновенной оси
вращения,

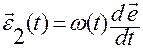· — угловое ускорение, возникающее из-за
изменения направления орта мгновенной
оси вращения.

В этих обозначениях формула для вращательного ускорения приобретает вид:

.

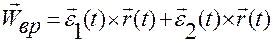Из нее следует, что вращательное ускорение при сферическом движении твердого тела не совпадает с 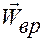при вращении твердого тела вокруг мгновенной оси вращения (напомним, что именно на этой оси точки твердого тела имеют скорость, равную нулю).

Обратимся теперь к вектору 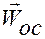(см. рис. 3.13.3).

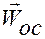
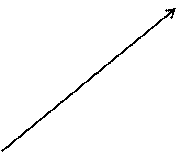
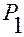
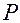
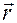
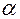
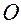
Рис. 3.13.3

Формула для ускорения 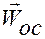приводится к следующей форме:

,

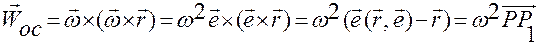т.е. 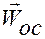при сферическом движении совпадает с осестремительным ускорением точки, которое она имеет при вращении вокруг неподвижной оси, если за неподвижную ось взять мгновенную ось вращения с направляющим ортом .

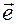5º. Теорема Эйлера-Даламбера

Пусть известна ориентация твердого тела в моменты времен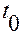и и 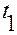. Справедлива следующая теорема.

Теорема 3 (Эйлера-Даламбера)

При сферическом движении произвольное положение твердого тела, заданное в момент 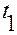, можно получить из заданного в момент 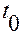начального положения одним поворотом вокруг неподвижной оси, проходящей через неподвижную точку 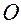, на некоторый угол .

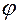Доказательство теоремы можно найти, например,
на стр.52-53 учебника: Маркеев А.П. Теоретическая механика, Москва: ЧеРо, 1999г., 572с.

Дата добавления: 2014-01-04