
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Гипербола
|
|
|
|
Эллипс
ЭЛЛИПС, ГИПЕРБОЛА, ПАРАБОЛА
ФИГУРЫ ВТОРОГО ПОРЯДКА
Фигуры, которые изучались в предыдущей главе, т.е. прямые и плоскости, задавались в аффинных реперах линейными уравнениями (уравнениями первой степени), поэтому они называются фигурами первого порядка. В этой главе мы рассмотрим фигуры второго порядка, которые в аффинных реперах задаются уравнениями второй степени. В первом параграфе познакомимся эллипсом и гиперболой, которые вместе с параболой являются важнейшими примерами фигур второго порядка.
Определение 3.1.2. Эллипсом называется фигурана плоскости 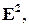 которая в некоторой прямоугольной системе координат
которая в некоторой прямоугольной системе координат  может быть задана уравнением
может быть задана уравнением
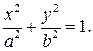 (1)
(1)
Здесь 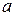 и
и 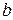 – фиксированные положительные числа, причем
– фиксированные положительные числа, причем 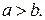
Уравнение (1) называется каноническим уравнением эллипса. Если 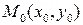 – точка эллипса, то из уравнения (1) вытекает, что
– точка эллипса, то из уравнения (1) вытекает, что  Это означает, что эллипс – ограниченная фигура, лежащая внутри прямоугольника размерами
Это означает, что эллипс – ограниченная фигура, лежащая внутри прямоугольника размерами 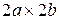 со сторонами параллельными осям координат и с центром в начале координат. Середины сторон прямоугольника
со сторонами параллельными осям координат и с центром в начале координат. Середины сторон прямоугольника 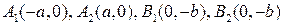 принадлежат эллипсу и называются вершинами эллипса. Числа
принадлежат эллипсу и называются вершинами эллипса. Числа 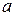 и
и 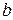 называются полуосями эллипса. Поскольку в уравнение (1) неизвестные
называются полуосями эллипса. Поскольку в уравнение (1) неизвестные 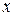 и
и 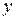 входят в квадратах, то вместе с любой точкой
входят в квадратах, то вместе с любой точкой 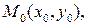 принадлежащей эллипсу, ему принадлежат точки
принадлежащей эллипсу, ему принадлежат точки 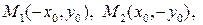
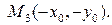 Это означает, что эллипс симметричен относительно осей координат и начала координат. Таким образом, чтобы нарисовать эллипс, достаточно изобразить его часть, лежащую в первой четверти, и затем достроить недостающие части, пользуясь симметрией. Считая, что
Это означает, что эллипс симметричен относительно осей координат и начала координат. Таким образом, чтобы нарисовать эллипс, достаточно изобразить его часть, лежащую в первой четверти, и затем достроить недостающие части, пользуясь симметрией. Считая, что  из уравнения (1) получаем, что в первой четверти эллипс задается графиком убывающей функции
из уравнения (1) получаем, что в первой четверти эллипс задается графиком убывающей функции

Правила построения графиков функций, известные из математического анализа, показывают, что это будет дуга кривой, выпуклой вверх, соединяющей вершины эллипса  и
и  . Используя симметрию, получаем изображение всего эллипса (рис. 1).
. Используя симметрию, получаем изображение всего эллипса (рис. 1).
|
|
|
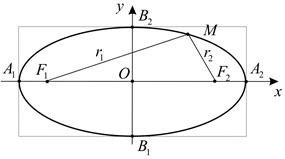
Рис. 1
Так как в уравнении (1) эллипса 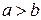 , можно определить число
, можно определить число 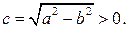 Отношение
Отношение 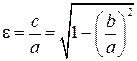 называется эксцентриситетом. Эксцентриситет эллипса – положительное число, меньшее единицы, характеризующее его форму. Если
называется эксцентриситетом. Эксцентриситет эллипса – положительное число, меньшее единицы, характеризующее его форму. Если 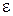 стремится к 0, то полуоси
стремится к 0, то полуоси 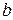 и
и 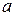 отличаются мало, и эллипс приближается к окружности, если
отличаются мало, и эллипс приближается к окружности, если 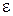 стремится к 1, то полуось
стремится к 1, то полуось 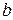 значительно меньше
значительно меньше 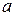 и эллипс приближается к отрезку (рис. 2).
и эллипс приближается к отрезку (рис. 2).
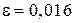

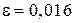
Рис. 2
Точки  и
и  называются фокусами эллипса. Если
называются фокусами эллипса. Если 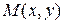 – произвольная точка эллипса, то отрезки
– произвольная точка эллипса, то отрезки 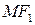 и
и 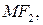 а также их длины
а также их длины 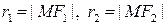 называются фокальными радиусами точки
называются фокальными радиусами точки 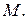 Вычислим значения фокальных радиусов:
Вычислим значения фокальных радиусов:
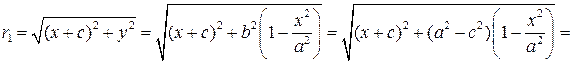
= 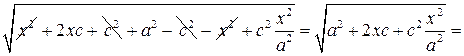
=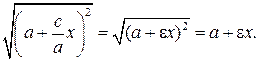
При извлечении последнего квадратного корня следует учесть, что 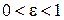 и для точки
и для точки 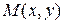 эллипса верно неравенство:
эллипса верно неравенство: 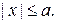 Аналогично,
Аналогично, 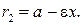 Заметим, что
Заметим, что 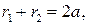 т.е. для любой точки эллипса с уравнением (1) сумма расстояний до фокусов постоянна и равна
т.е. для любой точки эллипса с уравнением (1) сумма расстояний до фокусов постоянна и равна 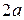 . Отмеченное свойство является характеристическим для эллипса. Это означает, что верно следующее утверждение.
. Отмеченное свойство является характеристическим для эллипса. Это означает, что верно следующее утверждение.
Теорема 3.1.1. Пусть 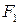 и
и 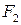 – две точки плоскости, расстояние между которыми равно
– две точки плоскости, расстояние между которыми равно 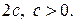 Тогда фигура
Тогда фигура 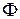 , состоящая из всех точек плоскости, для которых сумма расстояний до
, состоящая из всех точек плоскости, для которых сумма расстояний до 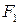 и
и 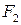 постоянна и равна
постоянна и равна  есть эллипс. Точки
есть эллипс. Точки 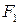 и
и 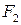 являются фокусами этого эллипса.
являются фокусами этого эллипса.
Доказательство. Выберем на плоскости прямоугольную систему координат 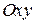 так, чтобы ось
так, чтобы ось 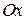 проходила через точки
проходила через точки 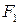 и
и 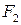 , а начало системы координат совпадало с серединой отрезка
, а начало системы координат совпадало с серединой отрезка 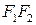 . В этой системе точки
. В этой системе точки 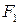 и
и 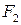 имеют следующие координаты:
имеют следующие координаты: 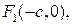
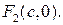 Пусть
Пусть 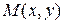 – произвольная точка плоскости. Тогда
– произвольная точка плоскости. Тогда
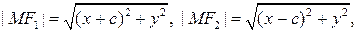
Следовательно, уравнение фигуры 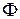 имеет вид:
имеет вид:
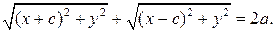 (2)
(2)
Перенесем второй корень в правую часть и возведем обе части уравнения в квадрат. Раскрывая скобки и приводя подобные, получим уравнение:
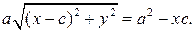
Еще раз возводим в квадрат обе части уравнения и приводим подобные:
|
|
|
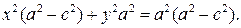
Так как по условию 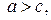 то можно определить число
то можно определить число 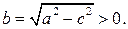 Разделив обе части последнего уравнения на
Разделив обе части последнего уравнения на 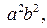 получим, что все точки фигуры
получим, что все точки фигуры 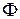 удовлетворяют уравнению эллипса:
удовлетворяют уравнению эллипса:
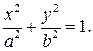 (1)
(1)
Выше было отмечено, что верно и обратное, т.е. любая точка эллипса удовлетворяет уравнению (1). Следовательно, фигура  является эллипсом. Точки
является эллипсом. Точки  и
и  , как отмечено выше, являются его фокусами.
, как отмечено выше, являются его фокусами.
Наряду с общим уравнением (1), часто используют параметрическое задание эллипса, которое получается следующим образом. Пусть  – прямоугольная система координат. Рассмотрим две концентрические окружности с центром в точке О и радиусами
– прямоугольная система координат. Рассмотрим две концентрические окружности с центром в точке О и радиусами 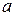 и
и 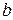 (рис. 3).
(рис. 3).
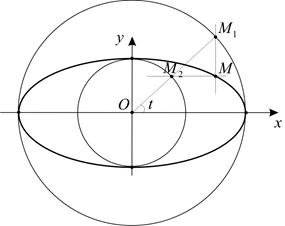
Рис. 3
Пусть 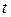 произвольное вещественное число. Из точки
произвольное вещественное число. Из точки 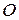 проведем луч, образующий угол
проведем луч, образующий угол 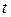 с положительным направлением оси
с положительным направлением оси 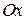 . Этот луч пересекает окружности в точках
. Этот луч пересекает окружности в точках  и
и 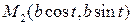 . Через точку
. Через точку 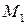 проведем прямую, параллельную оси
проведем прямую, параллельную оси 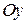 , а через точку
, а через точку 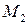 проведем прямую, параллельную оси
проведем прямую, параллельную оси 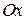 . Эти прямые пересекаются в точке
. Эти прямые пересекаются в точке 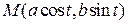 , которая, очевидно, лежит на эллипсе с уравнением (1). Если
, которая, очевидно, лежит на эллипсе с уравнением (1). Если 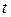 принимает все вещественные значения, то
принимает все вещественные значения, то 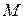 пробегает все точки эллипса, следовательно, параметрические уравнения эллипса имеют вид:
пробегает все точки эллипса, следовательно, параметрические уравнения эллипса имеют вид:
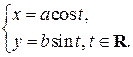
Определение 3.1.3. Гиперболой называется фигурана плоскости 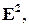 которая в некоторой прямоугольной системе координат
которая в некоторой прямоугольной системе координат 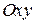 может быть задана уравнением
может быть задана уравнением
 (3)
(3)
Здесь 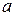 и
и 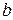 – фиксированные положительные числа.
– фиксированные положительные числа.
Уравнение (3) называется каноническим уравнением гиперболы. Если 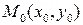 – точка гиперболы, то из уравнения (3) вытекает, что
– точка гиперболы, то из уравнения (3) вытекает, что  Это означает, что гипербола – фигура, лежащая вне полосы шириной
Это означает, что гипербола – фигура, лежащая вне полосы шириной 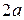 , которая определяется неравенством:
, которая определяется неравенством: 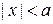 . Поскольку в уравнение (3) неизвестные
. Поскольку в уравнение (3) неизвестные 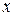 и
и 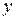 входят в квадратах, то гипербола, также как эллипс, симметрична относительно осей координат и начала координат. Таким образом, чтобы нарисовать гиперболу, достаточно изобразить ее часть, лежащую в первой четверти, и затем достроить недостающие части, пользуясь симметрией. Считая
входят в квадратах, то гипербола, также как эллипс, симметрична относительно осей координат и начала координат. Таким образом, чтобы нарисовать гиперболу, достаточно изобразить ее часть, лежащую в первой четверти, и затем достроить недостающие части, пользуясь симметрией. Считая 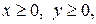 из уравнения (3) получаем, что в первой четверти гипербола задается графиком возрастающей функции
из уравнения (3) получаем, что в первой четверти гипербола задается графиком возрастающей функции

У этого графика есть наклонная асимптота с уравнением 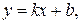 где
где
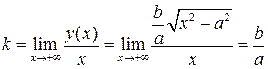 ,
, 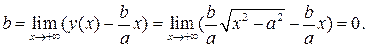
Далее нетрудно установить, что график функции представляет собой выпуклую вверх кривую, выходящую вертикально из точки  и асимптотически приближающуюся к прямой
и асимптотически приближающуюся к прямой  . Используя симметрию, получаем изображение всей гиперболы (рис. 5).
. Используя симметрию, получаем изображение всей гиперболы (рис. 5).
|
|
|
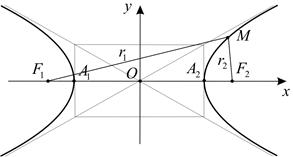
Рис. 5
Гипербола 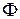 состоит из двух частей (ветвей), обозначим их:
состоит из двух частей (ветвей), обозначим их: 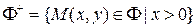 и
и 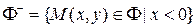 – соответственно правая и левая ветви на рисунке 5. Точки
– соответственно правая и левая ветви на рисунке 5. Точки 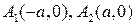 принадлежат гиперболе и называются ее вершинами. Числа
принадлежат гиперболе и называются ее вершинами. Числа 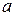 и
и 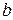 называются полуосями гиперболы,
называются полуосями гиперболы, 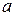 – действительная полуось,
– действительная полуось, 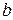 – мнимая полуось.
– мнимая полуось.
Для изображения гиперболы вручную на листе бумаги или на доске обычно поступают следующим образом. Вначале рисуют прямоугольник размерами 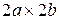 со сторонами параллельными осям координат и с центром в начале координат, такой же, как для эллипса с уравнением (1). Затем проводят асимптоты гиперболы
со сторонами параллельными осям координат и с центром в начале координат, такой же, как для эллипса с уравнением (1). Затем проводят асимптоты гиперболы 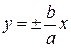 . Это прямые, на которых лежат диагонали основного прямоугольника. И наконец, рисуют ветви гиперболы
. Это прямые, на которых лежат диагонали основного прямоугольника. И наконец, рисуют ветви гиперболы  и
и  так, чтобы они касались основного прямоугольника в вершинах
так, чтобы они касались основного прямоугольника в вершинах  и
и 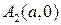 и асимптотически приближались к прямым
и асимптотически приближались к прямым 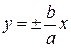 .
.
Определим число 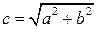 . Отношение
. Отношение 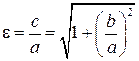 , также как для эллипса, называется эксцентриситетом. Эксцентриситет гиперболы – положительное число, большее единицы, характеризующее ее форму (
, также как для эллипса, называется эксцентриситетом. Эксцентриситет гиперболы – положительное число, большее единицы, характеризующее ее форму (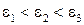 на рис. 6). Если
на рис. 6). Если 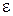 стремится к 1, то мнимая полуось
стремится к 1, то мнимая полуось 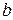 значительно меньше действительной полуоси
значительно меньше действительной полуоси 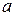 и гипербола приближается к двум лучам. Если
и гипербола приближается к двум лучам. Если 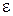 стремится к
стремится к  , то мнимая полуось
, то мнимая полуось 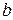 значительно больше действительной полуоси
значительно больше действительной полуоси 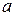 и гипербола приближается к паре параллельных прямых.
и гипербола приближается к паре параллельных прямых.
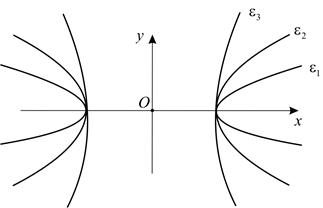
Рис. 6
У гиперболы с каноническим уравнением (3) имеются фокусы, это две точки:  и
и  (рис.). Если
(рис.). Если 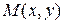 – произвольная точка гиперболы, то отрезки
– произвольная точка гиперболы, то отрезки 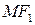 и
и 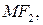 а также их длины
а также их длины 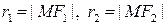 называются фокальными радиусами точки
называются фокальными радиусами точки 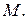 Вычислим значения фокальных радиусов:
Вычислим значения фокальных радиусов:
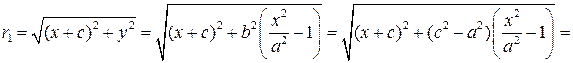
= 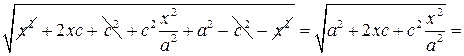
=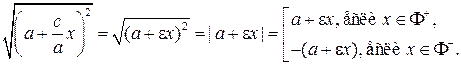
При извлечении последнего квадратного корня следует учесть, что 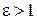 и для точки
и для точки 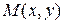 гиперболы
гиперболы 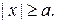 Аналогично,
Аналогично,

Заметим, что 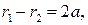
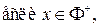 и
и 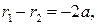
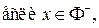 т.е. для любой точки гиперболы с уравнением (4) абсолютная величина разности расстояний до фокусов постоянна и равна
т.е. для любой точки гиперболы с уравнением (4) абсолютная величина разности расстояний до фокусов постоянна и равна 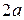 . Отмеченное свойство является характеристическим для гиперболы. Это означает, что верно следующее утверждение.
. Отмеченное свойство является характеристическим для гиперболы. Это означает, что верно следующее утверждение.
Теорема 3.1.2. Пусть 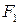 и
и 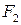 – две точки плоскости, расстояние между которыми равно
– две точки плоскости, расстояние между которыми равно 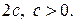 Тогда фигура
Тогда фигура 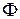 , состоящая из всех точек плоскости, для которых абсолютная величина разности расстояний до
, состоящая из всех точек плоскости, для которых абсолютная величина разности расстояний до 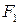 и
и 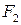 постоянна и равна
постоянна и равна 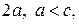 есть гипербола. Точки
есть гипербола. Точки 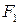 и
и 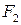 являются фокусами этой гиперболы.
являются фокусами этой гиперболы.
|
|
|
Доказательство. Выберем на плоскости прямоугольную систему координат 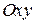 так, чтобы ось
так, чтобы ось 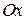 проходила через точки
проходила через точки 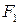 и
и 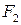 , а начало системы координат совпадало с серединой отрезка
, а начало системы координат совпадало с серединой отрезка 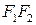 . В этой системе точки
. В этой системе точки 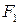 и
и 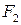 имеют следующие координаты:
имеют следующие координаты: 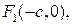
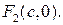 Пусть
Пусть 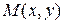 – произвольная точка плоскости. Тогда
– произвольная точка плоскости. Тогда
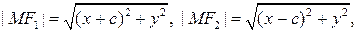
Следовательно, уравнение фигуры 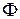 имеет вид:
имеет вид:
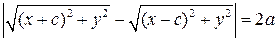 (4)
(4)
или
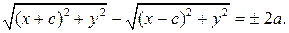
Перенесем второй корень в правую часть и возведем обе части уравнения в квадрат. Раскрывая скобки и приводя подобные, получим уравнение:
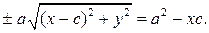
Еще раз возводим в квадрат обе части уравнения и приводим подобные:
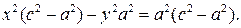
Так как по условию 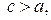 то можно определить число
то можно определить число 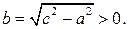 Разделив обе части последнего уравнения на
Разделив обе части последнего уравнения на 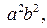 получим, что все точки фигуры
получим, что все точки фигуры 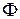 удовлетворяют уравнению гиперболы:
удовлетворяют уравнению гиперболы:
 (3)
(3)
Выше было отмечено, что верно и обратное, т.е. любая точка гиперболы удовлетворяет уравнению (4). Следовательно, фигура 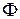 является гиперболой. Точки
является гиперболой. Точки 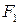 и
и 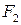 являются фокусами этой гиперболы.
являются фокусами этой гиперболы.
Наряду с гиперболой с уравнением (3) можно рассматривать гиперболу, которая задается уравнением
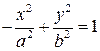 .
.
Эти две гиперболы называются сопряженными друг для друга. У сопряженных гипербол один и тот же основной прямоугольник и совпадают асимптоты, только действительные и мнимые оси меняются ролями (рис. 7).
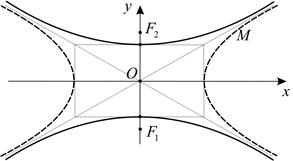
Рис. 7
Гиперболу можно задать параметрически. Соответствующие формулы подобны тем, которые использовались при задании эллипса, только обычные синус и косинус заменяются на гиперболические:
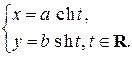 (5)
(5)
Поскольку 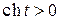 , то формулы (5) задают только одну ветвь гиперболы, вторая ветвь задается формулами:
, то формулы (5) задают только одну ветвь гиперболы, вторая ветвь задается формулами:

Для гиперболы с уравнением 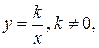 которая рассматривается в средней школе и является графиком обратно пропорциональной зависимости, оси координат являются асимптотами, а прямые с уравнениями
которая рассматривается в средней школе и является графиком обратно пропорциональной зависимости, оси координат являются асимптотами, а прямые с уравнениями 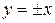 – осями симметрии. Каноническое уравнение такой гиперболы:
– осями симметрии. Каноническое уравнение такой гиперболы: 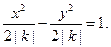
|
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 937; Нарушение авторских прав?; Мы поможем в написании вашей работы!