Определение сплайна. Интерполяционный кубический сплайн дефекта 1

Пусть на отрезке [а, b] задана упорядоченная система несовпадающих точек x_k (k =0, 1,..., n).

Определение 4.1. Сплайном S_m(x) называется определенная на [а, b] функция, принадлежащая классу С^l[а, b] l раз непрерывно дифференцируемых функций, такая, что на каждом промежутке [x_k-1, x_k] (k = l, 2,..., n) это многочлен т-й степени. Разность d = т - 1 между степенью сплайна т и показателем его гладкости l называется дефектом сплайна.

Если сплайн S_m(x) строится по некоторой функции f(x) так, чтобы выполнялись условия S_m(x_i) = f(x_i), то такой сплайн называется интерполяционным сплайном для функции f(x); при этом узлы сплайна x_k, вообще говоря, могут не совпадать с узлами интерполяции x_i.

Тривиальные примеры интерполяционных сплайнов можно построить виде кусочно-линейная функция y = a_kx + b_k с параметрами a_k, b_k, очевидно, является интерполяционным сплайном степени 1 дефекта 1, а кусочно-квадратичная функция y = a_kx² +b_kx +c_k, с непрерывной склейкой на концах промежутка интерполирования есть интерполяционный сплайн степени 2 дефекта 2.

Совпадение дефекта сплайна с его степенью обеспечивает просто непрерывность сплайна. Интерес представляет построение сплайнов с большей гладкостью, т.е. с малым дефектом. Такие сплайны являют собой дальнейшее совершенствование идеи кусочно-полиномиальной аппроксимации.

Рассмотрим наиболее известный и широко применяемый интерполяционный сплайн степени 3 дефекта 1. При этом будем исходить из предположения, что узлы сплайна

а = х₀, х₁ х₂,..., х_n= b (17.6)

одновременно служат узлами интерполяции, т.е. в них известны значения функции f_k:= f(x_k), k = 0,1,..., п.

Определение 4.2. Кубическим сплайном дефекта 1, интерполирующим на отрезке [а, b] данную функцию f(x), называется функция

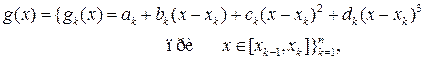(17.7)

удовлетворяющая совокупности условий:

а) g(x_k) = f_k (условие интерполяции в узлах сплайна);

б) g(x)ÎC² [а, b] (двойная непрерывная дифференцируемость);

в) g"(a) ⁼ g"(b) = 0 (краевые условия).

Определенный таким образом сплайн называют еще естественным или чертежным сплайном и связано это со следующим обстоятельством. Желая провести плавную линию через заданные точки плоскости, чертежники фиксировали в этих точках гибкую упругую рейку, тогда под влиянием упругих сил она принимала нужную форму, обеспечивающую минимум потенциальной энергии. Несложно убедиться, что определяемая условиями а)-в) функция (17.7), представляющая собой кубический п-звенник с гладким сопряжением звеньев, служит математическим описанием такого чертежного приема.

С этой целью достаточно показать, что функция g(x) доставляет минимум функционала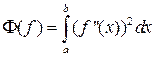, характеризующее величину потенциальной энергии закрепленной в (п + 1)-й точке (17.6) упругой рейки.

Для построения по данной функции f(x) интерполирующего ее сплайна (17.7) нужно найти 4п его коэффициентов a_k, b_k, c_k, d_k (k = 1, 2,..., n). Чтобы понять, имеется ли для этого достаточное количество связей, расшифруем фигурирующие в определении 4.2 условия а)-в) через функции g_k(x), составляющие g(x), имея в виду, что в любом внутреннем узле должны совпадать значения двух соседних звеньев сплайна и двух их первых производных.

Имеем:

из условий интерполяции а):

g₁(x₀) = f₀, g_k(x_k) = f_k при k = 1, 2,..., n;

из условий гладкой стыковки звеньев сплайна б):

g_k-1(x_k-1) = g_k(x_k-1),

g¢_k-1(x_k-1) = g¢_k(x_k-1),

g¢¢_k-1(x_k-1) = g¢¢_k(x_k-1),

при k = 2, 3,..., n;

из краевых условий в):

g¢₁(x₀) = 0, g¢_k(x_k) =0.

Как видим, условий оказалось 4n — ровно столько, сколько в записи сплайна (17.7) неизвестных коэффициентов. Подставляя сюда выражения функций и их производных через коэффициенты a_k, b_k, c_k, d_k при указанных значениях k и полагая для краткости

h_k= x_k- x_k-1

получаем детализированную систему связей

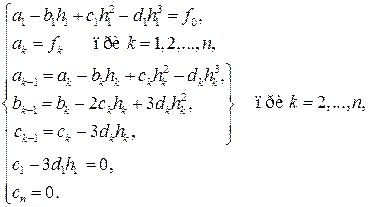(17.8)

Теперь ставим задачу выявления эффективного способа нахождения коэффициентов сплайна a_k, b_k, c_k, d_k (k = 1,2,...,n) из этой линейной относительно них системы (17.8). С этой целью будем исключать из системы неизвестные a_k, d_k, b_k и сводить все к решению системы относительно неизвестных c_k. При этом для упрощения записей используем уже применявшееся ранее обозначение разделенной разности

(17.9)

и, кроме того, введем фиктивный коэффициент

с₀=0.

Итак, согласно второго уравнения (17.8), коэффициенты a_k известны и равны f_k при любом k Î (1, 2,..., п). Подставляя их значения в первое и третье равенства (17.8), приходим к равенству

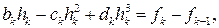
справедливому при k = 1, 2,..., n, откуда с учетом обозначения (17.9) получаем выражение

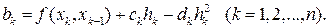(17.10)

Далее, из четвертого и пятого уравнеий (17.8)), если учесть (4.19), можно однозначно выразить d_k через c_k:

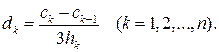(17.11)

С помощью (17.11) избавляемся от d_k в (17.10):

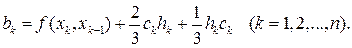(17.12)

Теперь используем четвертое равенство (17.8), подставляя туда b_k-1, b_k из (17.12) и d_k из (17.11):

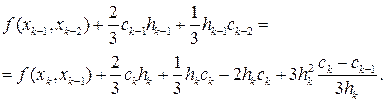
После упрощения отсюда получаем относительно неизвестных c_k трехточечное разностное уравнение второго порядка

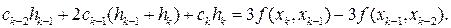(17.13)

где k = 2,3,..., п, с₀=0 и с_n=0 (согласно (17.8)).

Так как матрица системы (17.13) имеет диагональное преобладание (по другой терминологии, ленточной системы линейных алгебраических уравнений с трехдиагональной матрицей коэффициентов) выполняется достаточное условие однозначной разрешимости, т.е. существует единственный набор коэффициентов c₁, c₂,..., с_n, удовлетворяющий (17.13). Найдя эти коэффициенты, все остальные коэффициенты сплайна (17.7) так же однозначно получаем по формулам, (17.12) и (17.11). Таким образом, справедлива следующая

Теорема 17.1. При заданных в точках а и b краевых условиях (g¢¢ (a) = g"(b) = 0) по заданным в узлах (17.6) значениям f_k (k = 1, 2,..., n,) функции f(x) можно построить единственный интерполирующий ее кубический сплайн g(x) дефекта 1.

Следует отметить высокую технологичность процесса сплайн-интерполирования.

Действительно, упомянутое выше диагональное преобладание в трехдиагональной матрице системы (17.13) обеспечивает корректность и устойчивость метода прогонки. Применение этого метода для решения системы (17.13) сводится к вычислению прогоночных коэффициентов по формулам прямой прогонки

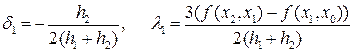
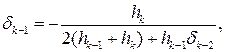
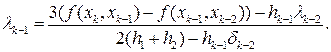
при k = 3, 4,...,n, а затем к получению искомых значений c_k обратной прогонкой по формуле

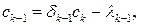
полагая в ней k = п, п - 1,..., 2 и учитывая, что с_n = 0. После этого, как уже говорилось, остается подставить c_k в выражения d_k (17.11) и b_k (17.12), а в качестве a_k в (17.7) взять значения f_k. Все вычислительные затраты на построение n-звенного естественного сплайна составят, очевидно, О(п) арифметических операций.

Факт и скорость сходимости сплайн-интерполяционного процесса характеризует следующее приводимое здесь без доказательства утверждение.

Теорема 17.2. Пусть g(x) — кубический сплайн дефекта 1, интерполирующий на системе узлов (17.6) отрезка [а, b] четырежды непрерывно дифференцируемую на нем функцию f(x). Тогда при любом фиксированном п найдется такая постоянная С > 0, что для любого х Î [а, b] справедливо неравенство:

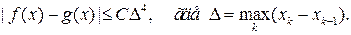
Все расчетные формулы упрощаются в частном случае, когда сплайн g(x) строится по системе равноотстоящих узлов.

Дата добавления: 2014-01-04