Функции Уолша. Основные определения. Способы упорядочения функций Уолша

Пол Фейерабенд (р. 1924).

Томас Кун (р. 1922).

Имре Лакатош (1921–1974).

Функции Уолща являются естественным расширением системы функций Радемахера, получены Уолшем в 1923 г. и представляют полную систему ортонормированных прямоугольных функций.

Множество функций Уолша, упорядоченных по частости, обычно обозначают следующим образом:

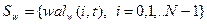
(17.1)

N=2ⁿ, n=1,2,3,... нижний индекс w показывает, что упорядочение осуществляется по Уолшу (по частости). Индекс функции i соответствует i-му элементу множества S _w. Обозначим через n_i частость функции wal _w (i,t). Для определения частости воспользуемся соотношением:

(17.2)

Функции Уолша, упорядоченные по частости, аналогично тригонометрическим функциям можно подразделить на четные cal(i,t) и нечетные sal(i,t)

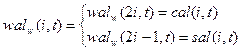
(17.3)

На рисунке 17.1 показаны первые восемь функций wal _w (i,t).

а)

б)

Рисунок 17.1

При этом видно, что частость каждой последующей функции Уолша больше или равняется частости предыдущей функции Уолша и имеет на одно пересечение нулевого уровня больше в открытом интервале tÎ[0,1]. Отсюда и следует название «упорядочение по частости».

Дискретизация функций Уолша, показанных на рисунке 17.1а, в восьми равноотстоящих точках приводит к матрице (8х8), показанной на рисунке 17.1б. Эту матрицу обозначают H _w (n) где n=log₂N и матрица будет иметь размер NxN.

Функции Уолша при упорядочении по частости в общем случае можно получать из функций Радемахера r_k(x) по формуле:

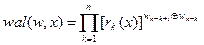
(17.4)

где w номер функции Уолша; k – номер функции Радемахера; показатель степени функции Радемахера, который принимает значение 0 или 1 в результате суммирования по модулю два, т.е. по правилу: 1Å1=0Å0=0; 1Å0=0Å1=1 разрядов двоичного числа w. Например для шестой функции Уолша (w =6), входящей в систему размером N=2³=8 произведение (17.4) состоит из трех сомножителей вида: при k=1 при k=2 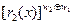при k=3 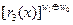. Число в двоичной системе записывается совокупностью нулей и единиц. В нашем случае значение w и его разрядов показаны в таблице 17.1

Таблица 17.1

Å Å Å

w	w0	w1	w2	w3	r1(x) ´ r2(x) ´ r3(x) = wal(w,x)
					r1^0(x) ´ r2^0(x) ´ r3^0(x) = wal(0,x)
					r1^1(x) ´ r2^0(x) ´ r3^0(x) = wal(1,x)
					r1^1(x) ´ r2^1(x) ´ r3^0(x) = wal(2,x)
					r1^0(x) ´ r2^1(x) ´ r3^0(x) = wal(3,x)
					r1^0(x) ´ r2^1(x) ´ r3^1(x) = wal(4,x)
					r1^1(x) ´ r2^1(x) ´ r3^1(x) = wal(5,x)
					r1^1(x) ´ r2^0(x) ´ r3^1(x) = wal(6,x)
					r1^0(x) ´ r2^0(x) ´ r3^1(x) = wal(7,x)

w ₀ – старший разряд числа, w ₃ – младший разряд числа w.

Показатели степени функций Радемахера получаются равными: 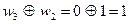; ; и следовательно,

wal(6,x)=r₁¹(x)×r₂⁰(x)×r₃¹(x)=r₁(x)r₃(x)

Правило получения показателей степеней для функции Радемахера схематически показано в таблице 17.1, где стрелками указаны суммируемые разряды числа w и функции Радемахера, к которым относится полученный показатель степени. Из рисунка 17.1 видно, что четные номера функций Уолша относятся к четным функциям, а нечетные к нечетным функциям. Другим способом упорядочения являются упорядочение по Пэли. При упорядочении по Пэли, аналитическая запись функции Уолша имеет вид:

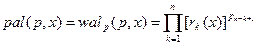
(17.5)

где p – двоичный номер функции, имеющий представление в двоичной форме:

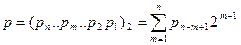
(17.6)

p₁ – младший разряд двоичного числа, р_n – старший разряд двоичного числа. При упорядочении по Пэли для формирования функций Уолша необходимо взять произведение возведенных в степень функций Радемахера, номера которых совпадают с номерами соответствующих разрядов двоихного представления числа р, а показатель степени каждой функции равен содержимому соответствующего разряда, т.е. 0 или 1. Причем младшей функции Радемахера соответствует младший разряд двоичной комбинации числа р. В соответствии с этим правилом в таблице 17.2 приведены значения функций Уолша упорядоченных по Пэли.

Таблица 17.2

р	р1	р2	р3	r1(x) × r2(x) × r3(x)	walp(i,x) = wal w (j,x)
				r1^0(x) × r2^0(x) × r3^0(x)	walp(0,x) = wal w (0,x)
				r1^1(x) × r2^0(x) × r3^0(x)	walp(1,x) = wal w (1,x)
				r1^0(x) × r2^1(x) × r3^0(x)	walp(2,x) = wal w (3,x)
				r1^1(x) × r2^1(x) × r3^0(x)	walp(3,x) = wal w (2,x)
				r1^0(x) × r2^0(x) × r3^1(x)	walp(4,x) = wal w (7,x)
				r1^1(x) × r2^0(x) × r3^1(x)	walp(5,x) = wal w (6,x)
				r1^0(x) × r2^1(x) × r3^1(x)	walp(6,x) = wal w (4,x)
				r1^1(x) × r2^1(x) × r3^1(x)	walp(7,x) = wal w (5,x)

Функции Радемахера в таблице показаны в форме: . Сравнение произведений и степеней функций Радемахера, записанных в таблицах 17.1 и 17.2 показывает., что между функциями Уолша, упорядоченными по Пэли и по Уолшу существует соответствие, которое отражено в последнем столбце таблицы 17.2. В соответсвии с функциями Уолша упорядоченными по Пэли также может быть построена матрица отсчетов H_p(n), аналогичная показанной на рисунке 17.1б.

Следующим распространенным способом упорядочения является упорядочение по Адамару. Функции Адамара har(h,x) формируют с помощью матриц Адамара. Матрицей Адамара H_N порядка N=2ⁿ называется квадратная матрица с размерами NxN и элементами ±1, обладающая свойством

(17.7)

где I – единичная матрица; 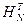– транспонированная матрица. Матрицы Адамара можно строить Используя рекурсивное соотношение:

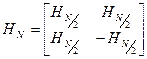
(17.8)

Например начиная с Н₁=1 находим:

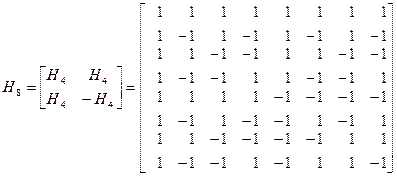
Сравнивая полученную матрицу Н₈ с матрицей отсчетов для функции Уолша, Упорядоченных по Уолшу (рисунок 17.1б) видим, что между первыми восемью функциями упорядоченными по Уолшу и Адамару существует следующее соответствие:

walh(0,x)=wal w (0,x); walh(2,x)=wal w (3,x); walh(4,x)=wal w (1,x); walh(6,x)=wal w (2,x);

walh(1,x)=wal w (7,x); walh(3,x)=wal w (4,x); walh(5,x)=wal w (6,x); walh(7,x)=wal w (5,x).

(17.9)

Дата добавления: 2014-01-04