Фактор-кольцо

ЛЕКЦИЯ 17

Понятие идеала 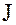кольца аналогично понятию нормального делителя H для группы G. Это позволяет подойти к построению фактор-кольца 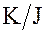таким же образом, как и при построении фактор-группы G/H.

Пусть 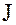– идеал кольца .

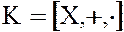Так как основу кольца составляет аддитивная абелева группа 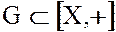, в качестве элементов фактор-кольца можно выбрать смежные классы 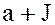, где 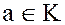, которые называются классами вычетов по модулю идеала кольца.

Теорема. Множество аддитивных смежных классов образуют фактор-кольцо 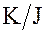с операциями:

1. 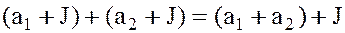(1)

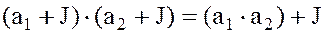2. (2)

Кроме того, естественное отображение 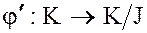вида 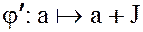является эпиморфизмом (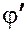– сюрьективно).

Доказательство. В абелевой группе 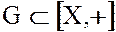любая подгруппа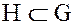нормальна, т.к. , поэтому выражение (1) определяет абелеву группу фактор-кольца , а отображение является эпиморфизмом аддитивных абелевых групп G и .

Остается проверить, что выражение (2) однозначно определяет операцию умножения на множестве аддитивных смежных классов , т.е. не зависит от выбора представителей соответствующих классов.

Пусть ,- представители двух смежных классов и , т.е.

,

тогда , где .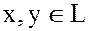

Найдем произведение

,

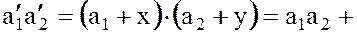
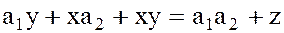где .

Остается показать, что .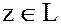

Действительно, т.к. 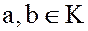и 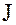– идеал в K, то ,

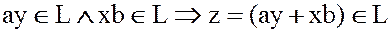т.к. .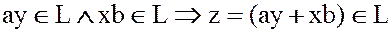

Поэтому находятся в одном смежном классе с элементами 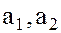, а это означает что произведение (2) определено правильно.

Пример. Рассмотрим кольцо целых чисел 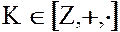. Идеалом этого кольца является , т.е. множество целых чисел, делящихся на m без остатка.

Аддитивный смежный класс кольца K по идеалу 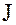имеет вид 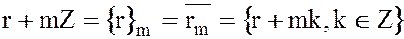, где .

Множество аддитивных смежных классов содержит ровно 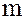классов вычетов по модулю 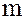, и они имеют вид:

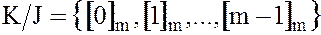
Таким образом, элементами фактор-кольца 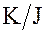являются классы вычетов по модулю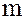

.

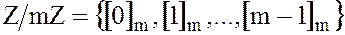Операции, на фактор-кольце задаются на классах вычетов, как и ранее:

,

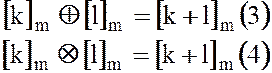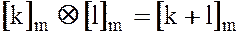
При фиксированном m будем, как и ранее, использовать сокращенные записи :

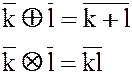
Понятие фактор-кольца 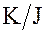по идеалу кольца 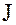позволяет сформировать основную теорему о гомоморфизме колец.

Дата добавления: 2014-01-04