Интерполяция с кратными узлами

Рассмотрим задачу полиномиальной интерполяции функции f (x) в более общей постановке.

Пусть на промежутке [ a, b ] расположены т + 1 несовпадающих узлов х ₀, х ₁,.., х_т, и пусть в этих точках известны значения у ₀ =f (х ₀), у ₁ =f (х ₁),..., y_m=f (x_m) данной функции, а также некоторые ее производные (максимальный порядок производных в разных узлах различен; в каких-то узлах производные могут быть вовсе неизвестны). Такие узлы будем называть кратными узлами. Конкретнее, будем считать, что заданы:

в узле х ₀ значения

в узле х ₁ значения 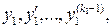(17.6)

…………………………………..

в узле х_т значения ;

тогда кратность узла х ₀ считается равной k ₀, узла х ₁ — k ₁ ,..., узла х_т — k_m.

Предполагая, что суммарная кратность узлов есть

k ₀ + k ₁ +... + k_m=n + 1, (17.7)

ставим задачу построения многочлена Н_n (х) степени п (не выше п), такого, что

(17.8)

где m >0, 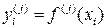— заданные через выражения (17.6) значения функции f (x) и ее производных, и по определению считается 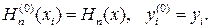Многочлен Н_п (х) будем называть интерполяционным многочленом Эрмшпа, а совокупность условий (17.8) — условиями эрмитовой интерполяции.

Формально можно считать, что нахождение такого многочлена состоит в том, чтобы однозначно определить n + 1 коэффициентов а ₀, а ₁..., а_n его канонического представления

H_n (x) = a ₀ + a ₁ x+ … + a_nxⁿ (17.9)

из условий (17.8). В силу предположения (17.7), совокупность требований (17.8) можно рассматривать как систему из п + 1 уравнения относительно п + 1 неизвестного — коэффициентов многочлена ((17.9).

Можно доказать существование и единственность многочлена Н_п (х), удовлетворяющего условиям эрмитовой интерполяции. Выявление общего вида интерполяционных многочленов Эрмита Н_п (х) представляет непростую задачу и требует привлечения определенных сведений из теории функций комплексной переменной. Рассмотрим одну из возможных процедур фактического построения таких многочленов, не требующую знания их общего вида.

Пусть L_m (x) — интерполяционный многочлен Лагранжа, построенный по данным т + 1 значениям f (х_k) = y_k, k = 0,1,..., т. Как и в лекции 16, будем пользоваться обозначением 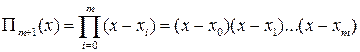. Так как по условию число т заведомо не превосходит n, то по теореме о делении многочлена с остатком искомый многочлен Эрмита H_n (x) можно представить в виде

H_n (x)= L_m (x) + H_{n- (m+ 1)}(x) ×P _{m+ 1}(x) (17.10)

где H_{n- ( m+ 1)}(x) — некоторый неизвестный пока многочлен степени п - т- 1.

Для построения многочлена H_{n- ( m+ 1)}(x) будем привлекать информацию о производных данной функции, т.е. равенства 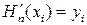в тех узлах х_i где первые производные, в соответствий с (17.6), заданы/

Продифференцировав равенство (17.10), имеем

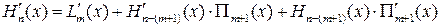. (17.11)

Так как P _{m+ 1}(x_i) = О, то в тех узлах x_i, где по условию эрмитовой интерполяции справедливо можно записать

.

Отсюда выражаем значения многочлена H_{n- ( m+ 1)}(x) узлах:

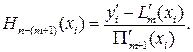
Правая часть этого равенства может быть вычислена; обозначим ее через z'_i. Таким образом, в ряде узлов x_i, известны значения многочлена H_{n- ( m+ 1)}(x_i) = z'_i, по которым этот многочлен однозначно восстанавливается обычной лагранжевой интерполяцией, если в условиях (17.6) содержится только производные порядка выше первого. Если же в исходной информации (17.6) имеются значения производных более высокого порядка, чем первый, то для восстановления многочлена H_{n- ( m+ 1)}(x_i) ставится задача эрмитовой же интерполяции, для чего, наряду с полученными его значениями z'_i, находят значения его производных путем дифференцирования равенства (17.11) (возможно неоднократного, в зависимости от максимального порядка заданных производных функцииЭта процедура построения интерполяционных многочленов Эрмита все более низких степеней продолжается до исчерпывания всей информации (17.8) о функции и ее производных.

Дата добавления: 2014-01-04