
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Правила знаходження визначених інтегралів
|
|
|
|
1. Формула Ньютона-Лейбніца:
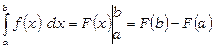 ,
,
де 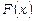 - первісна для
- первісна для 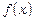 , тобто
, тобто 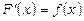 .
.
2. Інтегрування частинами:
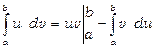
де 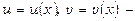 нескінченно диференційовані функції на відрізку
нескінченно диференційовані функції на відрізку 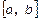 .
.
3. Заміна змінної:
 ,
,
де  функція, неперервна разом з усією похідної
функція, неперервна разом з усією похідної 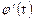 на відрізку
на відрізку 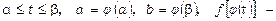 функція неперервна на
функція неперервна на  .
.
4. Якщо 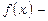 непарна функція, тобто
непарна функція, тобто 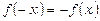 , то
, то
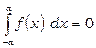 .
.
Якщо  парна функція, тобто
парна функція, тобто  , то
, то
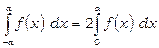 .
.
Приклади 22. 1) Обчислити інтеграл 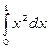 як границю інтегральної суми.
як границю інтегральної суми.
Тут 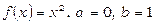 ; розділимо відрізок
; розділимо відрізок 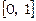 на п рівних частин, тоді
на п рівних частин, тоді 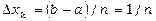 виберемо
виберемо 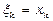 . Маємо:
. Маємо:
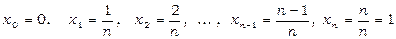 ;
;
 .
.
Отже,

 .
.
Тут використана формула суми квадратів натуральних чисел.
2) Обчислити  за формулою Ньютона-Лейбніца.
за формулою Ньютона-Лейбніца.
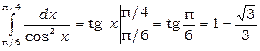 .
.
3) Оцінити інтеграл 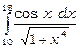 .
.
Оскільки  , то при
, то при 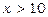 одержимо нерівність
одержимо нерівність 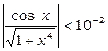 .
.
Отже,
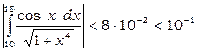 , тобто
, тобто 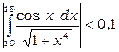 .
.
4) Оцінити інтеграл 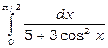 .
.
Оскільки 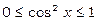 , маємо
, маємо
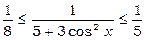 та
та 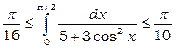 .
.
5) Обчислити  .
.
Скористаємося методом інтегрування частинами. Покладемо  , звідки
, звідки 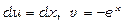 . Тоді
. Тоді
 .
.
6) Обчислити 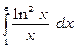 .
.
Покладемо 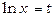 ; тоді
; тоді  ; якщо
; якщо 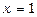 , то
, то 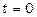 ; якщо
; якщо  , то
, то 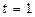 .
.
Отже,
 .
.
7) Обчислити 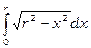 .
.
Покладемо 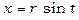 ; тоді
; тоді  ; якщо
; якщо  , то
, то 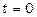 ; якщо
; якщо 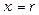 , то
, то 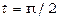 . Тому
. Тому
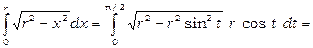
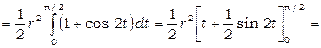
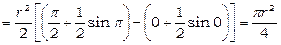 .
.
8) Обчислити 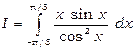 .
.
Підінтегральна функція – парна, а тому  . Інтегруємо частинами, покладаючи
. Інтегруємо частинами, покладаючи 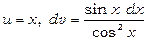 ; тоді
; тоді  . Звідси знаходимо
. Звідси знаходимо
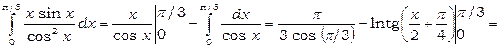
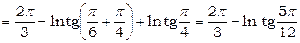 .
.
Отже, 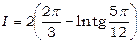 .
.
9) Обчислити 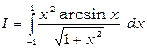 .
.
Підінтегральна функція – непарна, отже, 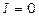 .
.
10) Обчислити інтеграл 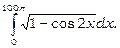
Маємо: 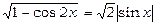 . Тому
. Тому 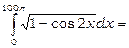
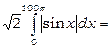
=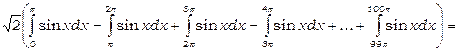
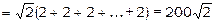 .
.
11) Чи можна застосувати формулу Ньютона-Лейбніця до інтеграла 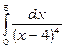 ?
?
Ні, не можна. Якщо формально обчислювати цей інтеграл за формулою Ньютона-Лейбніця, то одержимо невірний результат. Дійсно,
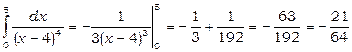 .
.
Але підінтегральна функція 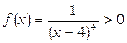 і, значить, інтеграл не може дорівнювати від’ємному числу. Сенс полягає в тому, що підінтегральна функція
і, значить, інтеграл не може дорівнювати від’ємному числу. Сенс полягає в тому, що підінтегральна функція 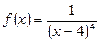 має нескінчений розрив у точці x =4, що належить проміжку інтегрування. Значить, тут формула Ньютона-Лейбніця не може бути застосована.
має нескінчений розрив у точці x =4, що належить проміжку інтегрування. Значить, тут формула Ньютона-Лейбніця не може бути застосована.
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 598; Нарушение авторских прав?; Мы поможем в написании вашей работы!