
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Приклади спряжених просторів
1. Нехай E – 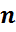 -вимірний лінійний простір (дійсний або комплексний). Оберемо в ньому який-небудь базис
-вимірний лінійний простір (дійсний або комплексний). Оберемо в ньому який-небудь базис 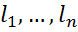 ; тоді всякий вибір
; тоді всякий вибір 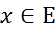 однозначно представимо у вигляді
однозначно представимо у вигляді

Якщо 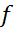 – лінійний функціонал на E, то ясно, що
– лінійний функціонал на E, то ясно, що
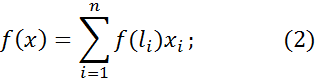
отже, лінійний функціонал однозначно визначається своїми значеннями на векторах базису 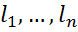 , причому ці значення можна задати довільно. Визначимо лінійні функціонали
, причому ці значення можна задати довільно. Визначимо лінійні функціонали 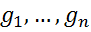 , вважаючи
, вважаючи
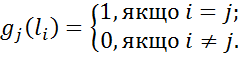
Очевидно, що ці функціонали лінійно-незалежні. Ясно, що 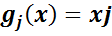 , тому формулу (2) можна записати у вигляді
, тому формулу (2) можна записати у вигляді

Таким чином, функціонали 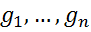 складають базис у просторі E*, тобто E* –
складають базис у просторі E*, тобто E* – 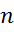 -вимірний лінійний простір, базис
-вимірний лінійний простір, базис 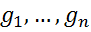 в E* називають двоїстим по відношенню до базису
в E* називають двоїстим по відношенню до базису 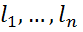 в E.
в E.
Різні нормі в просторі E індукують різні норми в E*. Ось декілька прикладів пар відповідних один одному в E і E*:
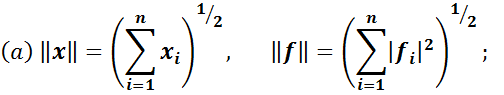
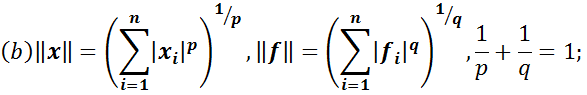
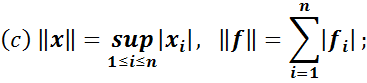
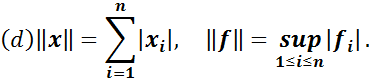
В цих формулах 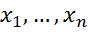 – це координати вектора
– це координати вектора 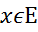 в базисі
в базисі 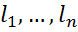 , а
, а 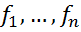 – координати функціонала
– координати функціонала 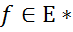 в двоїстому базисі
в двоїстому базисі 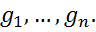
2. Розглянемо простір С0 послідовностей, що сходяться до нуля  з нормою
з нормою
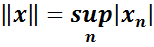
покажемо, що спряжений до нього простір (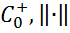 ) ізоморфний простору
) ізоморфний простору 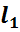 абсолютно підсумованих послідовностей
абсолютно підсумованих послідовностей 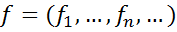 з нормою
з нормою
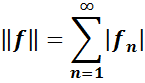
Будь-яка послідовність 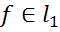 визначає в просторі С0 лінійний обмежений функціонал
визначає в просторі С0 лінійний обмежений функціонал 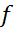 за формулою
за формулою
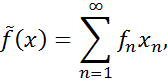
такою що
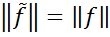 , (3)
, (3)
ясно, що

тому

Розглянемо в С0 вектори
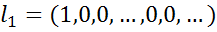 ;
;
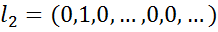 ;
;
…………………………
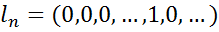 ;
;
……………………….
і покладемо
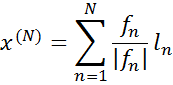
(якщо 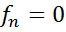 , то вважаємо, що
, то вважаємо, що  ). Тоді
). Тоді 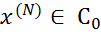 ,
, 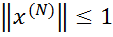 і
і
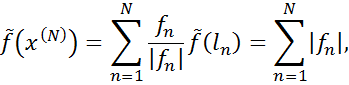
так, що

Внаслідок цього 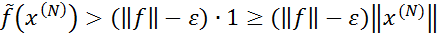 ,
,
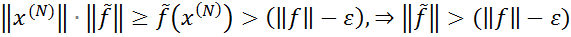 ,
,
в силу довільності 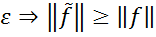 , тобто
, тобто
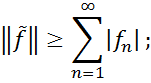
зіставляючи з доведеною вище протилежною нерівністю, робимо висновок, що
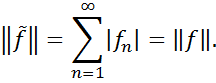
Таким чином, ми побудували лінійне ізометричне відображення 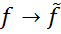 простору
простору  в простір
в простір  . Залишилось впевнитися в тому, що образ простору
. Залишилось впевнитися в тому, що образ простору  співпадає з усім
співпадає з усім  , тобто що будь-який функціонал
, тобто що будь-який функціонал  можна подати у вигляді (3), де
можна подати у вигляді (3), де 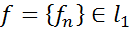 . Для будь-якого
. Для будь-якого 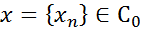 маємо
маємо
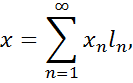
причому ряд, що стоїть праворуч, сходиться у 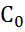 до елемента
до елемента 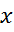 , бо
, бо
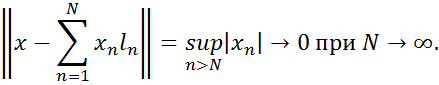
Так як функціонал  неперервний, то
неперервний, то
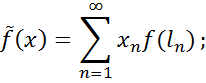
тому достатньо перевірити, що

Вважаючи, що
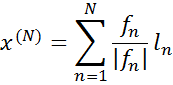
і вважаючи, що 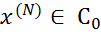 ,
, 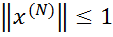 , маємо
, маємо

звідки в силу довільності 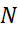 робимо висновок, що
робимо висновок, що
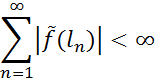
3. Неважко довести, що простір 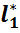 , спряжений з простором
, спряжений з простором  , ізоморфне з простором
, ізоморфне з простором 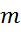 , що складається з усіх обмежених послідовностей
, що складається з усіх обмежених послідовностей 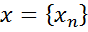 з нормою
з нормою
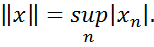
4. Нехай 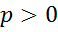 и
и 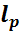 – простір всіх послідовностей
– простір всіх послідовностей 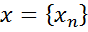 , для яких
, для яких
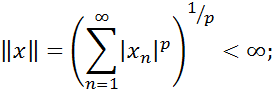
Можна довести, що спряжений до нього простір 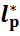 ізоморфний до простору
ізоморфний до простору 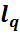 ,
, 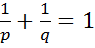 . Загальний вигляд неперервного лінійного функціонала на
. Загальний вигляд неперервного лінійного функціонала на 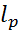 :
:
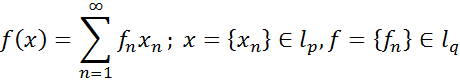
Доведення засноване на використанні нерівності Гельдера.
5. З’ясуємо структуру простору, спряженого до гільбертового.
Теорема: Нехай  – дійсний гільбертів простір. Для будь-якого неперервного лінійного функціонала
– дійсний гільбертів простір. Для будь-якого неперервного лінійного функціонала 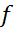 на
на  існує єдиний елемент
існує єдиний елемент 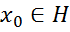 , такий що
, такий що
 , (4)
, (4)
причому  . Обернено, якщо
. Обернено, якщо 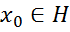 , то формула (4) визначає такий неперервний лінійний функціонал
, то формула (4) визначає такий неперервний лінійний функціонал 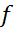 , то
, то  . Таким чином, рівність (4) визначає ізоморфізм
. Таким чином, рівність (4) визначає ізоморфізм 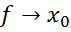 між просторами
між просторами 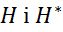 .
.
|
Дата добавления: 2014-01-04; Просмотров: 403; Нарушение авторских прав?; Мы поможем в написании вашей работы!