
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Бином Ньютона
|
|
|
|
Теорема. (a + b)n = 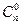 an +
an + an-1b +
an-1b +  an-2b2 +…+
an-2b2 +…+ 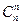 bn =
bn =
=  . Эта формула называется биномом Ньютона.
. Эта формула называется биномом Ньютона.
Первое доказательство (индукцией по п).
п = 1. Утверждение очевидно: (a + b)1 =  a1 +
a1 +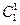 b1 = a + b.
b1 = a + b.
Пусть утверждение верно для п – 1. Докажем его для п.
(a + b)n = (a + b)×(a + b)n-1 =(a + b)× 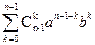 = =
= = +
+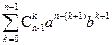

 +
+ = = aп +
= = aп +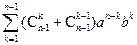 + bп
+ bп 
 .
.
Второе доказательство (для умных, но ленивых).
Раскроем скобки в выражении
(a + b)n = (a + b)×(a + b)×…× (a + b), (1.1)
выбирая из каждого двучлена справа или a или b, и записывая их в произведение с сохранением порядка множителей. Так, например произведение aababb… получится, если мы выберем из первого двучлена a, из 2-го a, из 3-го b, из 4-го a, из 5-го b, из 6-го b и т.д. Если мы теперь все множители a запишем слева, а множители b справа, то получим одночлен вида an-kbk. Все одночлены такого вида получаются при выборе из п двучленов в (1.1) подмножества (сочетания) из k двучленов, в которых при раскрывании скобок мы выбираем в качестве множителей элементы b (а из остальных двучленов, естественно, выбираются в качестве множителей элементы a). Количество таких подобных одночленов равно количеству сочетаний из n по k. Если мы их всех просуммируем, то получим слагаемое 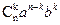 в разложении бинома Ньютона.
в разложении бинома Ньютона.
Утверждение 1.4.
а) 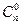 +
+ +
+ +…+
+…+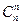 = 2 n,
= 2 n,
б) 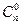 +
+ +
+ +…=
+…=  +
+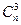 +
+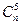 +…= 2 n-1
+…= 2 n-1
Доказательство а). Из бинома Ньютона при a = b =1
(1 + 1)n = 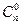 +
+  +
+  +…+
+…+ 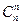 .
.
Доказательство а) для умных, но ленивых. Сумма
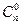 +
+ +
+ +…+
+…+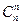 равна количеству всех подмножеств в множестве Х из п элементов, включая Æ и само множество Х.
равна количеству всех подмножеств в множестве Х из п элементов, включая Æ и само множество Х.
Это количество можно посчитать иначе. Для выделения любого подмножества в Х мы для каждого элемента из Х должны указать, входит этот элемент в наше подмножество или нет. Таким образом, для каждого элемента имеется 2 возможности – быть включенным в любое подмножество или нет, а для п элементов из Х имеется 2 n возможностей быть включенными или нет в различные подмножества. Включая или не включая произвольный элемент в подмножества, мы получаем различные подмножества. Таким образом, количество различных подмножеств в Х равно 2 n.
|
|
|
Упражнение. Доказать утверждение 1.4, б) с помощью формулы бинома Ньютона при a = 1, b = - 1.
Лекция 2.
- КОМПЛЕКСНЫЕ ЧИСЛА
Будем считать известными множества натуральных чисел N, целых чисел Z, рациональных чисел Q, действительных чисел R.
Определение. Комплексным числом будем называть упорядоченную пару действительных чисел (a,b), a,b Î R.
Множество комплексных чисел будем обозначать буквой С.
С = {(a,b), a,b Î R }.
I. Определим на множестве С операции:
1. по определению (a,b)+ (с,d) = (a+с, b+d) – операция сложения,
2. по определению (a,b)× (с,d) = (aс - bd, ad+bc) – операция умножения,
3. для с Î R по определению с× (a,b)= (ca, cb) – операция умножения комплексных чисел на действительные.
II. Утверждение. Для определенных на С операций выполняются свойства:
1. (z1 + z2) + z3 = z1 +(z2 + z3) " z1, z2, z3 Î C, z1 =(a1,b1),
z2 = (a2,b2), z3 = (a3,b3),
2. $ элемент 0 С = (0,0)Î C такой, что 0 С +z = z + 0 С = z " zÎ C. 0 С называется нейтральным элементом в C по сложению.
3. " z Î C, z =(a,b), $ z¢ Î C такой, что z+ z¢ = 0 С. В самом деле, z¢ = (- a, - b). z¢ обозначается как - z и называется элементом, противоположным к z.
4. z1 + z2 = z2 + z1 " z1, z2 Î C,
5. (z1 z2) z3 = z1 (z2 z3) " z1, z2, z3 Î C,
6. $ элемент 1 С = (1,0)Î C такой, что 1 С × z = z × 1 С = z " zÎ C. 1 С называется нейтральным элементом в С по умножению или единицей.
7. " z Î C, z ¹ 0 С, z =(a,b), $ z1 Î C такой, что z z1 = 1 С. В самом деле, z1 = (a/(a2 + b2), - b/(a2 + b2)). z1 обозначается как z-1 и называется элементом, обратным к z.
8. z1 z2 = z2 z1 " z1, z2 Î C,
9. (z1 +z2)z3 = z1 z3 + z2 z3, z1(z2 + z3)= z1 z2+ z1z3 " z1, z2, z3Î C.
i. c(z1 + z2) = cz1 + cz2 " z1, z2 Î C, " c Î R,
ii. (c + d)z = cz + dz " c, d Î R, " zÎ C,
iii. (c d)z = c(dz) " c, d Î R, " zÎ C,
|
|
|
iv. 1 С z = z " zÎ C.
Очевидно, все эти свойства следуют из определений операций и свойств действительных чисел, которые мы считаем известными.
Упражнение. Доказать свойства 1 ¸ 9 и i ¸ iv.
Множество (не обязательно числовое), на котором
I. определены операции, обозначаемые знаками + и ×,
II. и для которых выполнены свойства 1 ¸ 9, называется полем.
Очевидно, полями являются множества Q и R. Теперь мы видим, что множество С также является полем.
Обозначим число (0, 1)Î C буквой i. Число i называется мнимой единицей. Очевидно, " zÎ C, z = (a,b) = a (1, 0) + + b (0, 1)= a× 1 С + b i. Обычно единицу в качестве множителя не пишут. Поэтому и мы будем записывать число z в виде
z = a + b i, а единицу 1 С, когда это не вызовет недоразумений, мы будем записывать в виде 1.
Легко видеть, что i2 = - 1. Для комплексного числа z = a + b i будем называть комплексное число a - b i комплексно сопряженным к z и обозначать  . Очевидно,
. Очевидно,
а)  =
= +
+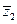 , б)
, б) 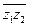 =
= 
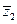 , в) z
, в) z  = a2 + b2.
= a2 + b2.
Определение. Модулем комплексного числа z = a + b i называется число | z | = .
.
Так как z  = | z | 2, то | z1 z2 | 2 = z1z2
= | z | 2, то | z1 z2 | 2 = z1z2 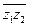 = z1z2
= z1z2 
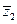 = | z1 | 2 | z2 | 2,
= | z1 | 2 | z2 | 2,
и | z1 z2 | = | z1 | ×| z2 |.
Комплексное число a + b i можно изображать точкой на плоскости с координатами (a, b) или вектором на плоскости с координатами (a, b). Легко видеть, что комплексные числа складываются как векторы по правилу параллелограмма (или по правилу треугольника). Очевидно (см. рис.),
a + b i = r cosj +r sinj ×i = r(cosj +i sinj).

Запись комплексного числа в виде r(cosj +i sinj) называется тригонометрической формой записи. Угол j называется аргументом комплексного числа (определен неоднозначно). Очевидно, r = | z |.
Легко проверить, что r1(cosj1+i sinj1)× r2(cosj2+i sinj2)=
= r1r2(cos(j1+j2)+i sin(j1+j2)). Отсюда следует
формула Муавра: (cosj +i sinj)n = cos nj + i sin nj,
а также ещё раз мы получаем, что | z1 z2 | = r1r2 = | z1 | ×| z2 |.
|
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 1873; Нарушение авторских прав?; Мы поможем в написании вашей работы!