Кратные корни многочлена

Замечания.

Следствия.

1. (х^k)¢ = k х^k-1 " k Î N.

2. (а_пх ^п+ а_п-1х ^п-1+…+ а₀)¢= nа_пх ^п-1+(n – 1)а_п-1х ^п-2+…+ а₁.

1. Во всех наших формулах kb = b+b+…+b – сумма из k слагаемых.

2. Формулы для производных многочленов у нас получились такие же, как и в математическом анализе. Надо лишь только учитывать, что если char P ¹ 0, то некоторые слагаемые могут быть равны 0. Так например, если char P = р, то (х^р)¢ = 0.

Далее в 10.7 будем считать, что char P = 0.

Определение. Пусть f(x)= p(x)^kg(x), где p(x) - простой многочлен в P [x], и p(x) не делит g(x). Тогда k – называется кратностью множителя p(x) в разложении f(x). Если k ³ 2, то множитель p(x) называется кратным. Если р(х) = х – а, то есть f(x)= (x – а)^kg(x), и (х – а) не делит g(x), то k – называется кратностью корня а многочлена f(x). Если k ³ 2, то корень а называется кратным, а если k = 1, то корень а называется простым.

Теорема. Если кратность простого множителя p(x) в раз-

ложении f(x) равна k, то кратность p(x) в разложении f¢(x) равна k – 1.

Доказательство. Так как f¢(x)=kp(x)^k-1p(x)¢g(x)+p(x)^kg(x)¢= = p(x)^k-1(kp(x)¢g(x)+p(x)g(x)¢), то p(x)^k-1 | f¢(x). Покажем, что p(x) не делит (kp(x)¢g(x)+p(x)g(x)¢). В самом деле, если мы предположим, что p(x)| (kp(x)¢g(x)+p(x)g(x)¢), то получим, что p(x)| (kp(x)¢g(x)). Но p(x) и g(x) – взаимно простые Þ p(x)| p(x)¢ - противоречие, так как ст.p(x)¢ = ст.p(x) – 1.

ÿ

Теорема. У f(x) существуют кратные простые множители тогда и только тогда, когда f и f¢ не взаимно простые.

Доказательство. Пусть f(x)= р₁р₂…р_s- разложение f на простые множители. Тогда f¢(x)= р₁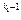р₂… р_sh(x), и h(x) не делится на р_i "i. Следовательно, D= р₁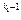р₂…р_s является наибольшим общим делителем для f и f¢. Таким образом, f и f¢ не взаимно простые, то есть D ¹ 1 Û $ k_i> 1.

ÿ

Если необходимо решить уравнение f(x)= 0, и многочлен f(x) содержит кратные множители, то мы можем перейти к эквивалентному уравнению меньшей степени следующим образом. С помощью алгоритма Евклида найдем D – наибольший общий делитель для f и f¢. Затем разделим f на D:

f ¤ D = р₁р₂…р_s. Очевидно, уравнение f ¤ D = 0 эквивалентно первоначальному уравнению, то есть имеет те же корни. Операция перехода к уравнению f ¤ D = 0 называется освобождением от кратных множителей или освобождением от кратных корней.

Дата добавления: 2014-01-04