Прямая сумма линейных операторов

Прямая сумма инвариантных подпространств.

Пусть j: Lⁿ ® Lⁿ - линейный оператор, Lⁿ=L₁ Å L₂ - пря­мая сумма j- инвариантных подпространств L₁ и L₂ ,

е¢ ={е₁,…,е_m} – базис в L₁, е¢¢ ={е_m+1,…,е_n} – базис в L₂, dimL₁= m, dimL₂= n - m. Тогда е = {е₁,…,е_m,е_m+1,…_,е_n} – ба­зис всего пространства Lⁿ, и в этом базисе из инвариантности L₁ матрица [ j ] имеет вид (16.1). Но мы можем утверждать и большее. Так как L₂ – также j- инвариантно, то "j =m+1,…,n j е_jÎ L₂, то есть j е_j = 0е₁+…+0е_m + a _m+1,j е_m+1+…+a_nj е_n Þ в матрице (16.1) В = 0, то есть

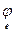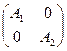
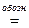[ ] =А₁ ∔ А₂ - (16.2)

распавшаяся или блочно-диагональная матрица. Здесь А₁ – квадратная матрица порядка m, А₂ - квадратная матрица по­рядка n – m, А₁ = 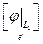, А₂ = .

Обратно, если в некотором базисе е матрица [ 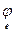] имеет

вид (16.2), то Lⁿ=L₁ Å L₂ - прямая сумма j- инвариантных подпространств L₁ и L₂ , где L₁= <е₁,…,е_m>, L₂= <е_m+1,…, е_n>.

Вывод: Lⁿ распадается в прямую сумму j- инвариантных

подпространств Û [ 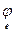] в некотором базисе е имеет блочно- диагональный вид (16.2).

Пусть Lⁿ=L₁ Å … Å L_k и "i=1,…,k определен ли­нейный оператор j _i: L_i® L_i c матрицей [ 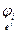] в базисе е ⁱ={е₁ ⁱ,…,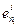} подпространства L_i.

Теорема. $! линейный оператор j: Lⁿ ® Lⁿ такой, что 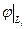= j _i.

Доказательство.

1. Единственность. Пусть искомый л.о. j существует. Тогда "хÎ Lⁿ, х = х₁+…+ х_k, где все х_iÎ L_i, и j х = j х₁+…+j х_k = = j₁ х₁+…+ j_k х_k – отсюда следует единственность л.о. j.

2. Существование. Определим линейный оператор j: Lⁿ® Lⁿ так: пусть "хÎ Lⁿ, х = х₁+…+ х_k ( где все х_iÎ L_i),

j хj₁ х₁+…+ j_k х_k (из пункта 1 видно, что никак иначе определить л.о. j мы и не можем). Тогда

j х_i=j(0+…+ х_i+…+0)=j₁0+…+j_iх_i+…+j_k0= j_i х_i, то есть "i имеем j|_Li=j _i. Из линейности операторов j _i легко следует линейность оператора j.

Упражнение. Доказать линейность оператора j.

ÿ

Определение. Построенный линейный оператор j называется прямой суммой линейных операторов j₁,…,j_k и обозначается j₁ ∔ … ∔ j_k или j₁ Å … Å j_k.

В базисе е пространства Lⁿ, полученном объединением базисов е ¹,…, е ^k, матрица [ 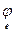] = [ ]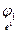∔ … ∔[ 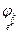]. Кроме того, можно увидеть, что все F(L_i) (см. п. 13.5) естественным образом инъективно вкладываются в F(Lⁿ), сумма их в F(Lⁿ) является прямой:

F(Lⁿ)É F(L₁) Å … Å F(L_k), и j₁ ∔ … ∔ j_k ÎF(L₁) Å … Å F(L_k).

В случае прямой суммы двух j- инвариантных подпространств Lⁿ=L₁ Å L₂ получаем j = j|_L1 ∔ j|_L2.

Дата добавления: 2014-01-04