Структура эрмитова оператора

Лемма. Пусть j: Н^п® Н^п - эрмитов оператор, Н^п É L –

j- инвариантное подпространство. Тогда L ^{^} - j- инвариантное подпространство.

Доказательство. " хÎ L, y Î L ^{^} (j x, y) = 0 = (x,j y) Þ j(L ^{^} ) ^ L Þ j(L ^{^} )Í L ^{^}.

ÿ

Как и в теореме из п.22.3 Н^п=L₁ Å L₂ Å…Å L_п , где все L_i – подпространства размерности 1, j- инвариантны и попарно ортогональны.

Если L – унитарное пространство размерности 1, L= <e>, и j: L ® L - эрмитов оператор, то j е = a е, aÎ С Þ

(j е,е)= (a е,е)= a(е,е)= (е, j е)= (е, a е)= 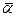(е,е) Þ a =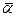Þ aÎ R.

В разложении Н^п = L₁ Å L₂ Å…Å L_n выберем в каждом L_i единичный вектор и_i. Объединение и этих векторов является ортонормированным базисом в Н^п. В этом базисе матрица эрмитова оператора j имеет вид: [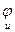] = diag(a₁,,…,a_n), где все a_sÎ R. Таким образом, нами доказана структурная

Теорема. Для любого эрмитова оператора j: Н^п ® Н^п $ ортонормированный базис и евклидова пространства, в котором матрица j имеет вид: [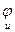] = diag(a₁,a₂,…,a_n), где все a_sÎ R. Наоборот, если [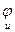] = diag(a₁,…,a_n), где все a_sÎ R, то j - эрмитов.

На языке матриц теорему можно сформулировать так:

Для любой эрмитовой матрицы А $ унитарная матрица

Т (матрица перехода к новому ортонормированному базису) такая, что матрица Т ^-1АТ = diag(a₁,a₂,…,a_n), где все a_sÎ R.

Определение. Линейный оператор j в евклидовом или унитарном пространстве называется нормальным, если

j*j = jj*.

Заметим, что ортогональные и унитарные операторы –

нормальные, так как j*j = jj* = id, самосопряженные и эрмитовы операторы – нормальные, так как j* = j.

Можно доказать структурную теорему для нормальных операторов, а затем, как частные случаи, получить из неё структурные теоремы, которые мы доказали для ортогональных, самосопряженных, унитарных, эрмитовых операторов.

Лекция 34.

Дата добавления: 2014-01-04