Наслідок. Якщо і — дві довільні точ­ки і точка — середина відрізка , тобто , то і формула (3) набирає вигляду

Де — координати точки, — координати точки.

. (4)

Приклад. Дано точки і 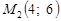. Відрізок, обмежений цими точками, поділяється у відношенні . Знайти координати точки ділення .

Ø За формулами (3) знаходимо:

; .

Таким чином, 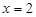, 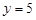— координати точки поділу.

1. На осі Ox, знайти точку, відстань якої від точки А (3; 4) дорів­нює 5.

Відповідь. (6; 0) і (0; 0).

2. Точка М є серединою відрізка ОА, що сполучає початок координат О з точкою А (–5; 2). Знайти координати точки М.

Відповідь. (–5/2; 1).

3. Точка М (2, 3) поділяє відрізок АВ у відношенні 1:2. Знайти координати точки В, коли відомо, що точка А має координати х = 1, у = 2.

Відповідь. В(4; 5).

4. Вершинами трикутника є точки А (–2; 1), В (2; 2), С (4; у). Площа трикутника дорівнює 15. Визначити ординату вершини С.

Відповідь. ; .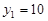

5. Знайти координати центра мас однорідної пластинки, що має форму трикутника з вершинами А (–2; 1), В (2, –1), С (4; 3).

Відповідь. 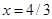; у = 1.

Вказівка. Центр мас трикутника міститься в точці перетину його медіан, що поділяє кожну з медіан у відношенні 2:1, лічачи від вершини.

6. Площа трикутника дорівнює 3, дві його вершини — точки А (3; 1) і В(1; –3). Знайти координати третьої вершини, коли відомо, що вона лежить на осі ординат.

Відповідь. С(0; –8) чи С(0; 2).

7. Площа паралелограма дорівнює 12, дві його вершини — точ­ки А (–1; 3) і В (–2; 4). Знайти дві інші вершини паралелограма, коли відомо, що точка перетину його діагоналей лежить на осі абсцис.

Відповідь. C₁(–7; –3), або , D₂(18; –4).

8. Вершини трикутника — точки А (3; 6), В (–1; 3) і С (2; –1). Знайти довжину його висоти, проведеної з вершини С.

Відповідь. 5.

1. Вивести формулу відстані між двома точками.

2. Довести формулу площі трикутника. В якому разі права частина формули, змінює знак на протилежний?

3. Вивести формули координат точок розподілу відрізка в даному відношенні. В якому разі координати точок поділу дорівнюють півсумі відповідних координат?

3. Полярна система координат

Полярна система координат складається з деякої точки О, що називається полюсом, і променя ОЕ, що виходить з неї і називається полярною віссю. Крім того, задається одиниця масштабу для вимірювання довжин відрізків.

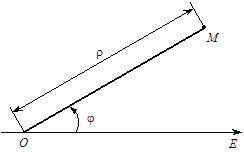
Рис. 1

Нехай задано полярну систему координат і нехай М — довільна точка площини. Позначимо через r відстань від точки М до точки О 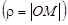, а через j — кут, на який потрібно повернути проти годинникової стрілки полярну вісь для суміщення її з променем ОМ (рис. 1).

Полярними координатами точки М називаються числа r і j. Число r вважають першою координатою і називають полярним радіусом, число j — другою координатою і називають полярним кутом.

Точка М із полярними координатами r і j позначається так: .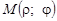

Зазвичай вважають, що полярні координати r і j змінюються в таких межах:

.

Проте іноді доводиться розглядати кути, більші за 2p, а також від’ємні кути, тобто кути, відлічувані від полярної осі за годинниковою стрілкою.

Встановимо зв’язок між полярними координатами точки і її прямокутними координатами, припускаючи, що початок прямокутної системи координат збігається з полюсом, а додатна піввісь абсцис — з полярною віссю. Нехай точка М має прямокутні координати х і у і полярні координати r і j (рис. 2):

, . (1)

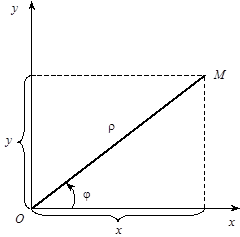
Рис. 2

Очевидно, за допомогою формул (1) прямокутні координати точки подаються через полярні, а вираз полярних координат через прямокутні випливає з формули (2) і має такий вигляд:

. (2)

Формула визначає два значення полярного кута j, оскільки j змінюється від 0 до 2p. Із цих двох значень кута j вибирають те, при якому задовольняються рівності(1).

Приклад. У прямокутній системі координат дано точку (2; 2). Знайти її полярні координати, вважаючи, що полюс сполучено з початком прямокутної системи координат, а полярна вісь збігається з додатною піввіссю абсцис.

Ø За формулами (2) знаходимо , . Відповідно до другої з цих рівностей 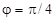або 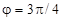. Оскільки х > 0 і у >0, то варто взяти 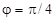. Отже, , .

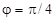Приклад. У полярній системі координат дано точку (2; p/4). Знайти її прямокутні координати, вважаючи, що полюс сполучено з початком прямокутної системи координат, а полярна вісь збігається з додатною піввіссю абсцис.

Ø За формулами(1) знаходимо: , 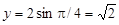. Отже, , .

1. У прямокутній системі координат дано точки M ₁(0; 5), М ₂(–3; 0), М ₃1). Знайти їхні полярні координати.

Відповідь. M ₁(5; p/2), M ₂(3; p), М ₃(2; p/6).

2. У полярній системі координат дано точки А (4; p/2) і В (8, –p/4). Знайти їхні прямокутні координати.

Відповідь. А (0; 4), В 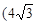; –4).

3. У полярній системі координат дано точки А (8; 2p/3) і В (6; p/3). Знайти полярні координати середини відрізка, що сполучає точки А і В.

Відповідь. (1; 2p/3).

1. Що називається системою координат?

2. Що таке полярні координати точки?

3. В яких межах змінюються полярні координати?

4. Вивести формули, що встановлюють зв’язок між полярними координатами точки та її прямокутними координатами.

4. Множини точок на площини та їхні рівняння

З’ясуємо далі, як в аналітичній геометрії за допомогою рівнянь можна знайти ту чи іншу множину точок на площині.

Такими множинами можуть бути одна чи кілька точок, лінія чи область на площині.

Той факт, що числа x і y є координатами точок, які належать деякій множині, аналітично записується у вигляді рівняння.

У багатьох задачах потрібно знайти множину точок (х; у), координати яких задовольняють задане рівняння. Відповідями в таких задачах є, як правило, фігури, добре відомі зі шкільного курсу геометрії. Головне — встановити, яка це фігура, і з’ясувати, які властивості вона має.

Означення рівняння лінії

Розглянемо співвідношення виду

F (х, у) = 0, (1)

що пов’язує змінні величини х і у. Рівність виду (1) називатимемо рівнянням із двома змінними х і у, якщо ця рівність справджується для деяких пар чисел х і у.

Приклади рівнянь:

, , .

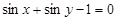Якщо рівність (1) справджується для всіх пар чисел х і у, то вона називається тотожністю.

Приклади тотожностей:

, .

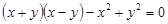Рівняння(1) називатимемо рівнянням множини точок (х; у), якщо його задовольняють координати х і у будь-якої точки множини і не задовольняють координати жодної точки, що не належить цій множині.

Рівняння (1) називається рівнянням лінії L (у заданій системі координат), якщо його задовольняють координати х і у будь-якої точки, що лежить на лінії L, і не задовольняють координати жодної точки, що не лежить на цій лінії.

З означення випливає, що лінія L являє собою множину всіх тих точок площини (х; у), координати яких задовольняють рівняння(1).

Якщо (1) є рівнянням лінії L, то будемо говорити, що рівняння (1) визначає (задає) лінію L.

Поняття «рівняння лінії» дає змогу зводити геометричні задачі до алгебраїчних. Наприклад, задача на відшукання точки перетину двох ліній, заданих рівняннями х + у = 0 і х ² + y ² = l, зводиться до алгебраїчної задачі спільного розв’язування цих рівнянь.

Лінія L може визначатися не тільки рівнянням виду (1), а й рів­нянням виду

,

що містить полярні координати.

Приклад. Вивести рівняння (у заданій прямокутній системі координат) множини точок, кожна з яких віддалена від точки 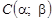на відстань R (рис. 1).

Рис. 1

Іншими словами, потрібно знайти рівняння кола радіуса R із центром у точці C (a; b).

Ø Вивести рівняння множини точок — означає знайти залежність між координатами будь-якої точки цієї множини.

Позначимо через М змінну точку, що належить даній множині точок, а через х, у — її поточні координати; тоді з умови випливає, що 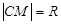. За формулою для відстані між двома точками маємо:

.

Підносячи обидві частини рівності до квадрата, дістаємо рівняння кола з центром у точці і радіусом R:

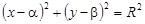. (2)

Воно зустрічається в багатьох геометричних задачах.

Узявши в рівності (2) a = 0, b = 0, дістанемо рівняння кола з центром у початку координат:

. (3)

Приклад. Знайти рівняння множини точок, рівновіддалених від точок А (1; 1) і В (3; 3).

Ø Візьмемо довільну точку М (х; у), що належить даній множині точок; тоді з умови випливає, що | МА | = | МВ |. Використовуючи формулу відстані між двома точками, знаходимо:

,

.

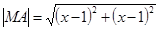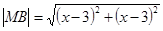Таким чином,

.

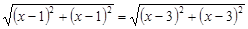Після перетворень дістаємо шукане рівняння множини точок; рівновіддалених від точок А (1; 1) і В (3; 3):

х + у – 4 = 0.

Як відомо з елементарної геометрії, такою множиною точок є пряма, що проходить через середину відрізка, який сполучає дані точки, і перпендикулярна до цього відрізка.

1. Дано точки M ₁(2; –2), М ₂(2; 2), М ₃(2; –1), М ₄(3; –3), М ₅(5; –5), M ₆(3; –2). Встановити, які з них лежать на лінії, заданій рівнянням х + у = 0, і які не лежать на ній.

Відповідь. Точки М ₁, М ₄ і М ₅ лежать на даній лінії; точки М ₂, М ₃ і М ₄ не лежать на ній.

2. Дано точки , , , , 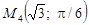. Встановити, які з них лежать на лінії, що визначається рівнянням 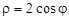, і які не лежать на ній.

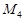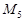Відповідь. Точки і лежать на даній лінії; точки і не лежать на ній. Рівняння визначає коло з діаметром .

3. Скласти рівняння лінії, по якій рухається точка М (х; у), рівновіддалена від точок А (0; 2) і В (4; –2).

Відповідь. х – у – 2 = 0.

4. Скласти рівняння лінії, відстань кожної точки якої від точки А (0; 1/4) дорівнює відстані цієї самої точки від прямої у = –1/4.

Відповідь. у =х².

5. Знайти рівняння множини точок, сума відстаней кожної з яких від точок F ₁(2; 0) і F ₂(–2; 0) дорівнює .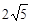

Відповідь. .

6. Знайти рівняння множини точок, рівновіддалених від точки А (2; 2) і осі Ох.

Відповідь. .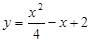

7. Знайти рівняння множини точок, рівновіддалених від осі Оу і точки А (4; 0).

Відповідь. .

8. Скласти рівняння лінії, яку описує середина відрізка з довжиною d, один кінець якого переміщується по осі абсцис, а другий — по осі ординат.

Відповідь. .

Насамкінець зауважимо, що в аналітичній геометрії розв’язують дві основні задачі: 1) за заданою лінією (множиною точок) знайти рівняння цієї лінії; 2) за заданим рівнянням деякої лінії визначити цю лінію та вивчити її геометричні властивості (форму і розміщення).

1. Що називається рівнянням із двома змінними і що називається тотожністю? Наведіть приклади.

2. Що називається рівнянням множини точок (х; у)?

3. Дайте означення рівняння лінії і самої лінії. Наведіть приклади.

4. Виведіть рівняння кола з центром у даній точці.

5. Які дві основні задачі розв’язуються в аналітичній геометрії? Проілюструйте прикладами.

5. Пряма та види її рівнянь

Рівняння прямої з кутовим коефіцієнтом

Нехай дано деяку пряму, не перпендикулярну до осі Ох. Назвемо кутом нахилу даної прямої до осі Ох кут a, на який потрібно повернути вісь Ох, щоб її додатний напрям збігся з одним із напрямів прямої. Кут a може набувати різних значень, що відрізняються один від одного на ±n p, де n — натуральне число. Як правило, за кут нахилу беруть найменше від’ємне значення кута a, на який потрібно повернути (проти годинникової стрілки) вісь Ох, щоб її додатний напрям збігся з одним з напрямів прямої (рис. 1). У цьому разі

Тангенс кута нахилу прямої до осі Ох називають кутовим коефіцієнтом цієї прямої і позначають:

k = tg a. (1)

З рівності (1) випливає, зокрема, що коли a = 0, тобто пряма паралельна осі Ох, то k = 0. Якщо , тобто пряма перпендикулярна до осі Ох, то вираз k = tg a втрачає сенс. У такому разі кажуть, що кутовий коефіцієнт перетворюється на нескінченність.

Виведемо рівняння прямої, знаючи її кутовий коефіцієнт k і величину b відрізка OB, який вона відтинає на осі Оу (див. рис. 1).

Нехай М — довільна точка площини з координатами х і у. Проведемо прямі BN і NM, паралельні координатним осям, і діста­немо прямокутний трикутник BNM.

Рис. 1

Точка М лежить на прямій тоді і тільки тоді, коли NM і BN задовольняють умову

.

Але NM = CM – CN = CM – OB = y – b, BN = x. Звідси згідно з формулою (1) дістаємо, що точка М (х; у) лежить на даній прямій тоді і тільки тоді, коли її координати задовольняють рівняння

,

яке після перетворень набирає вигляду

y = kx + b. (2)

Рівняння (2) називають рівнянням прямої з кутовим коефіцієн­том. Якщо k = 0, то пряма паралельна осі Ох і її рівняння має вигляд у = b.

Отже, рівняння будь-якої прямої, не перпендикулярної до осі Ох, має вигляд (2). Очевидно, правильне й обернене твердження: будь-яке рівняння виду (2) визначає пряму, що має кутовий коефіцієнт k і відтинає на осі Оу відрізок, величина якого b.

Приклад. Скласти рівняння прямої, що відтинає на осі Оу відрізок b = 3 і утворює з віссю Ох кут a = p/6.

Ø Знаходимо кутовий коефіцієнт:

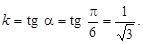
Підставивши k і b в рівність (2), дістанемо шукане рівняння прямої:

або .

Приклад. Побудувати пряму, задану рівнянням .

Ø Відкладемо на осі Оу відрізок ОВ, величина якого дорівнює 2 (рис. 2); проведемо через точку В паралельно осі Ох відрізок, величина якого BN = 4, і через точку N паралельно осі Оу відрізок, величина якого NM = 3.

Рис. 2

Після цього проводимо пряму ВМ, що і є шуканою. Вона має даний кутовий коефіцієнт k = 3/4 і відтинає на осі Оу відрізок
b = 2.

Рівняння прямої, що проходить через дану точку
і має даний кутовий коефіцієнт

Часто доводиться складати рівняння прямої, знаючи одну її точку 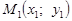і кутовий коефіцієнт k. Запишемо рівняння прямої у вигляді (2), де b — поки що невідоме число. Оскільки пряма проходить через точку 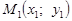, то координати цієї точки задовольняють рівняння (2): 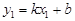. Виразивши з цієї рів­ності b і підставивши його в рівняння (2), дістанемо шукане рівняння:

. (3)

Зауваження. Якщо пряма проходить через точку 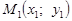перпендикулярно до осі Ох, тобто її кутовий коефіцієнт перетворюється на нескінченність, то рівняння має вигляд 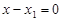. Формально це рівняння можна дістати з рівняння (3), поділивши обидві частини рівняння (3) на k і далі спрямувати k до нескінченності.

Приклад. Скласти рівняння прямої, що проходить через точку М (2; 1) і утворює з віссю Ох кут .

Ø Знаходимо кутовий коефіцієнт: 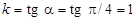. Підставивши координати точки М і значення кутового коефіцієнта k у рівність (3), дістаємо шукане рівняння прямої:

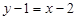або .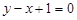

Рівняння прямої,
що проходить через дві дані точки

Нехай дано дві точки 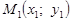і .

Беручи в рівнянні(3) точку за , маємо:

.

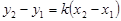Виразивши з останньої рівності k і підставивши його в рівняння (3), дістанемо шукане рівняння:

.

Це рівняння за умови, що , можна записати так:

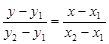(4)

Якщо , то рівняння шуканої прямої має вигляд 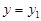. У цьому випадку пряма паралельна осі Ох. Якщо , то пряма паралельна осі Оу і її рівняння має вигляд .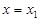

Приклад. Скласти рівняння прямої, що проходить через точки і .

Ø Підставивши координати точок і у рівність (4), діста­немо шукане рівняння прямої:

або .

Загальне рівняння прямої

Дата добавления: 2014-01-04