Теорема о разложении морфизма

Пусть Н - нормальная подгруппа в группе G, G / Н –

факторгруппа. Рассмотрим отображение a: G ® G / Н та-

кое, что "gÎ G a(g) = .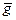

Утверждение. a - эпиморфизм групп, причем Ker a = H.

Доказательство. Так как " a, bÎ G a(ab) = = =

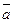
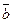= a(a)a(b), то a - морфизм групп. И конечно же, a - сюръекция, то есть a - эпиморфизм. Этот эпиморфизм a называется каноническим и обозначается сап. Очевидно, g Î Ker a Û 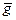=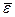Û g~ e Û gÎН. Следовательно, Kera = Ker сап =H.



Следствие. Мы видели, что ядро любого морфизма – нормальная подгруппа. Теперь мы увидели, что любая нормальная подгруппа является ядром некоторого морфизма, например, канонического. Таким образом, нормальные подгруппы – это в точности те подгруппы, которые являются ядрами некоторых морфизмов.

Пусть теперь j: G₁ ® G₂ - морфизм групп, Н = Kerj, G₁/ Н – факторгруппа, сап: G₁ ® G₁ / Н – канонический эпиморфизм.

Определим отображение : G₁ / Н ® G₂ следующим

образом: пусть по определению (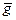) = jg " 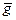Î G₁ / Н. Наше определение корректно, так как 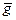= gH, и j(gH)= =jgj(H) = jg×e₂ = jg. Кроме того, " 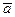,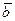Î G₁ / Н

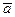
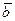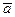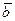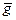() = () = j(ab) =jajb = () (), то есть - морфизм групп. Если Î Ker , то (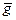) = jg = e₂ Þ

g Î Ker j = H Þ 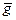= Þ Ker = {} Þ - инъекция (см. п.28.3, утверждение 3). Следовательно, - мономорфизм групп. И наконец, если мы будем рассматривать не как отображение G₁/ Н в G₂, а как отображение G₁/ Н в Imj = j(G₁), то будет ещё и сюръекцией, то есть и биекцией. Таким образом, : G₁ / Н ® Imj - изоморфизм групп. Так как Imj Í G₂, то обозначим через i тождественное вложение i: Imj ® G₂, i(g) = g "g Î Imj. Очевидно, i – морфизм и инъекция, то есть мономорфизм. Кроме того,

"gÎ G₁ (i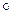 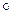can)(g) = i( (can(g)))= i( (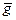)) = i(jg)= jg Þ i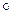 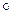can = j. Таким образом, нами доказана

Теорема о разложении морфизма. Если j: G₁ ® G₂ - морфизм групп, то коммутативна следующая диаграмма:

, то есть i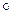 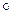can = j,

причем сап – эпиморфизм, - изоморфизм, i - мономорфизм групп.

Следствие. Для того, чтобы найти факторгруппу G / H группы G по нормальной подгруппе Н достаточно найти морфизм j группы G такой, что Ker j = H. И тогда

G / H» Im j.

Пример. Пусть G = С * - (коммутативная) группа ненуле-

вых комплексных чисел по умножению, Н=U_n= {zÎ C | zⁿ= 1} – множество корней п -й степени из 1.

Пример. Доказать, что U_n - подгруппа в С * (и следовательно, нормальная подгруппа).

Найдем G / H = С */ U_n. Для этого рассмотрим отображение j: С * ® С * такое, что " z Î C * j z = zⁿ. Очевидно,

1. j - морфизм (эндоморфизм группы C *), так как j(z₁z₂)= = (z₁z₂)ⁿ = z₁ⁿz₂ⁿ = j z₁j z₂.

2. Ker j = H = U_n. Отсюда, в частности, следует Упражнение.

3. Im j = C *, так как " иÎ C * $ zÎ C * такой, что и = zⁿ=j z. Следовательно, С */ U_n» С *.

Дата добавления: 2014-01-04