Модель Леонтьєва багатогалузевої економіки

(міжгалузевий баланс)

Нехай 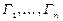– галузі виробництва, валовий обсяг продукції кожної галузі, позначимо, відповідно, 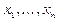. Обсяг кінцевого продукту галузі для невиробничого (ринкового) використання, відповідно, .

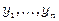Взаємодію галузей у процесі функціонування описують коефіцієнти прямих витрат 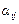– доля продукції галузі 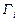на виробництво одиниці продукції галузі 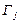, Очевидно, 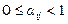(тобто значно менше одиниці), .

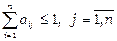У цих позначеннях обсяг продукції галузі 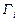на виробництво всієї продукції 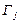буде дорівнювати 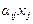. Сумарний обсяг витрат галузі 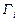на виробництво продукції всіх галузей (на виробниче використання) дорівнює .

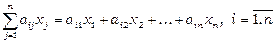Таким чином, для збалансованого функціонування галузей повинно виконуватись наступні співвідношення балансу:

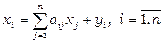. (3.6)

Оскільки 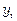можна інтерпретувати як ринковий попит на продукцію галузі 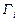, то рівність порушуватись не може. Інакше, або галузь 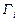буде виробляти зайвий продукт (нерівність 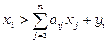), на зберігання якого потрібно витрачати додаткові кошти, або продукту галузі 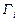не буде вистачати для задоволення потреб інших галузей та задоволення ринкового попиту (нерівність ).

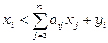З алгебраїчної точки зору співвідношення (3.6) є неоднорідною системою n лінійних рівнянь з n невідомими 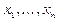. Для запису цієї СЛР у матричному вигляді, введемо наступні позначення:

матриця 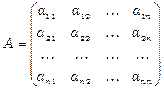називається матрицею прямих витрат або структурною матрицею економіки;

вектор-стовпчик 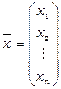називається вектором валового випуску;

вектор-стовпчик 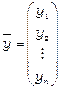називається вектором кінцевого продукту або ринкового попиту.

Отже, співвідношення балансу (10) набувають вигляду

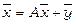. (3.7)

Побудована модель дозволяє розв’язати наступні задачі.

1. При заданій матриці прямих витрат А знайти вектор (скласти план виробництва для підприємств галузей), при якому задовольняється заданий ринковий попит 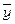. Для цього співвідношення (11) перетворимо наступним чином:

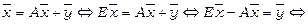
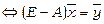(3.8)

Припустимо, що матриця (Е – А) – невироджена, тобто 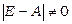. Тоді існує, причому єдина обернена до неї матриця 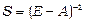, яка називається матрицею повних витрат. Її елементи 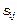можна інтерпретувати, як величину валового випуску продукції галузі 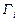, необхідної для забезпечення одиниці кінцевого продукту галузі 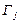. Отже, шуканий вектор знаходиться множенням обох частин співвідношення (14) на матрицю S, маємо

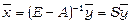. (3.9)

2. Яким умовам повинна задовольняти матриця прямих витрат А (умови на взаємодію галузей) для того, щоб ринковий попит на продукцію галузей міг бути задоволений у будь-яких пропорціях, тобто при яких умовах на матрицю А для кожного вектора попиту 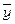(з невід’ємними координатами) можна знайти відповідний вектор валового випуску (з невід’ємними координатами).

Матриця А називається продуктивною, якщо для будь-якого вектора 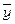(з невід’ємними координатами) існує розв’язок матричного рівняння (3.9) (з невід’ємними координатами).

Одним з критеріїв продуктивності матриці є наступне твердження.

Твердження. Якщо сума елементів кожного стовпчика матриці не перевищує одиниці (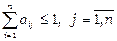), причому хоча б одна з цих сум строго менше одиниці, то матриця А – продуктивна.

Приклад 4. Скласти план випуску продукції галузями 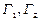для задоволення ринкового попиту на продукцію галузей 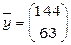за умови, що матриця прямих витрат має вигляд 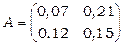(очевидно, ця матриця є продуктивною).

.

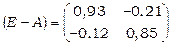Матриця повних витрат має вигляд

.

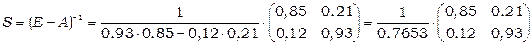Отже, за формулою (13) шуканий вектор має вигляд:

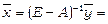
Таким чином, для задоволення ринкового попиту на свою продукцію галузь 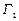повинна виробляти 169,8 одиниць продукції, а галузь 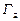–116,1 одиниць продукції.

3.4. Лінійна модель обміну (модель міжнародної торгівлі)

Нехай 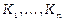– країни, що приймають участь у міжнародній торгівлі, об’єм коштів, що витрачає кожна країна на міжнародну торгівлю, позначимо, відповідно, 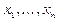. Коефіцієнти 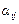– доля коштів, що витрачає країна 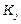на закупівлю товарів у країни 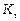. Очевидно, що

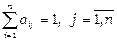. (3.10)

Розглянемо матрицю, складену з цих коефіцієнтів 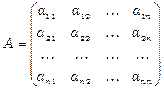. Ця матриця описує взаємодію країн в процесі міжнародної торгівлі та має назву структурної матриці торгівлі. Співвідношення (3.10) означає, що сума елементів кожного стовпчика цієї матриці дорівнює 1.

Дохід кожної країни 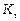від внутрішньої та зовнішньої торгівлі, очевидно, складає

.

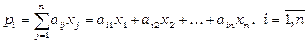Збалансовану торгівлю забезпечує бездефіцитність торгівлі кожної країни 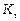, тобто дохід від торгівлі кожної країни повинен бути не менше об’єму коштів, що вкладає країна на міжнародну торгівлю: .

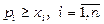Припустимо, що хоча б для однієї країни ця нерівність виконується як строга. Не порушуючи загальності, можна вважати, що нерівність виконується як строга для країни 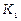. Тоді маємо систему нерівностей:

.

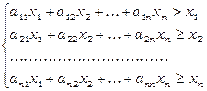Додамо всі нерівності системи, після групування отримаємо:

.

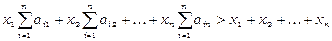Завдяки співвідношенням (3.10), маємо: 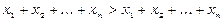– отримали протиріччя, отже припущення було невірним, і для збалансованої торгівлі повинні виконуватись рівності

.

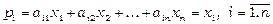З алгебраїчної точки зору маємо систему n лінійних рівнянь з n невідомими, яку можна записати у наступному матричному вигляді:

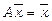, (3.11)

де 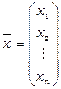– вектор-стовпчик коштів, що вкладаються країнами у міжнародну торгівлю.

Висновок. Для збалансованої торгівлі між країнами вектор коштів повинен бути власним вектором структурної матриці торгівлі А, що відповідає власному значенню 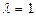(можна показати, що за виконання умов (14) матриця А завжди має власне значення ).

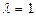Приклад 5. Нехайструктурна матриця торгівлі трьох країн 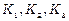має вигляд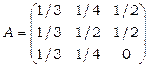

Знайти вектор коштів, які повинні вкладати країни для збалансованої торгівлі.

Знайдемо шуканий вектор як власний вектор даної матриці, що відповідає власному значенню 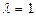, як розв’язок однорідної СЛР 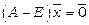. Для цього скористаємось методом Гауса.

.

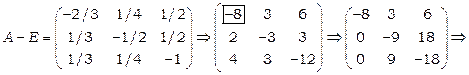
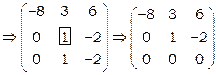Однорідна СЛР, що відповідає останній матриці, має вигляд: 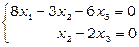. Покладемо вільну змінну 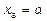, тоді , .

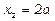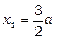Отже, .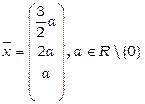

Отриманий результат означає, що для збалансованої торгівлі даних трьох країн об’єми коштів, що виділяються ними на торгівлю повинні знаходитись у співвідношенні 3:4:2.

Дата добавления: 2014-01-04