Сбалансированные по высоте деревья

В худшем случае, когда дерево вырождено в линейный список, хранение данных в упорядоченном бинарном дереве никакого выигрыша в сложности операций по сравнению с массивом или линейным списком не дает. В лучшем случае, когда дерево сбалансировано, для всех операций получается логарифмическая сложность, что гораздо лучше. Идеально сбалансированным называется дерево, у которого для каждой вершины выполняется требование: число вершин в левом и правом поддеревьях различается не более чем на 1.

Однако идеальную сбалансированность довольно трудно поддерживать. В некоторых случаях при добавлении или удалении элементов может потребоваться значительная перестройка дерева, не гарантирующая логарифмической сложности. В 1962 году два советских математика: Г.М. Адельсон-Вельский и Е.М. Ландис – ввели менее строгое определение сбалансированности и доказали, что при таком определении можно написать программы добавления и/или удаления, имеющие логарифмическую сложность и сохраняющие дерево сбалансированным. Дерево считается сбалансированным по АВЛ (сокращения от фамилий Г.М. Адельсон-Вельский и Е.М. Ландис), если для каждой вершины выполняется требование: высота левого и правого поддеревьев различаются не более, чем на 1. Не всякое сбалансированное по АВЛ дерево идеально сбалансировано, но всякое идеально сбалансированное дерево сбалансировано по АВЛ.

При операциях добавления и удаления может произойти нарушение сбалансированности дерева. В этом случае потребуются некоторые преобразования, не нарушающие упорядоченности дерева и способствующие лучшей сбалансированности.

Рассмотрим такие преобразования. Пусть вершина a имеет правый потомок b. Обозначим через P левое поддерево вершины a, через Q и R – левое и правое поддеревья вершины b соответственно. Упорядоченность дерева требует, чтобы . Точно того же требует упорядоченность дерева с корнем b, его левым потомком a, в котором P и Q – левое и правое поддеревья вершины a, R – правое поддерево вершины b. Поэтому первое дерево можно преобразовать во второе, не нарушая упорядоченности. Такое преобразование называется малым правым вращением (рис. 3). Аналогично определяется симметричное ему малое левое вращение.

Рис. 3. Малое правое вращение АВЛ-дерева

Пусть b – правый потомок вершины a, c – левый потомок вершины b, P – левое поддерево вершины a, Q и R – соответственно левое и правое поддеревья вершины c, S – правое поддерево b. Тогда . Такой же порядок соответствует дереву с корнем c, имеющим левый потомок a и правый потомок b, для которых P и Q – поддеревья вершины a, а R и S – поддеревья вершины b. Соответствующее преобразование будем называть большим правым вращением (рис. 4). Аналогично определяется симметричное ему большое левое вращение.

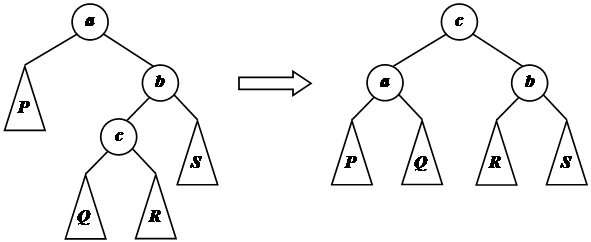Рис. 4. Большое правое вращение АВЛ-дерева

Схематично алгоритм добавления нового элемента в сбалансированное по АВЛ дерево будет состоять из следующих трех основных шагов.

Шаг 1. Поиск по дереву.

Шаг 2. Вставка элемента в место, где закончился поиск, если элемент отсутствует.

Шаг 3. Восстановление сбалансированности.

Первый шаг необходим для того, чтобы убедиться в отсутствии элемента в дереве, а также найти такое место вставки, чтобы после вставки дерево осталось упорядоченным. Третий шаг представляет собой обратный проход по пути поиска: от места добавления к корню дерева. По мере продвижения по этому пути корректируются показатели сбалансированности проходимых вершин, и производится балансировка там, где это необходимо. Добавление элемента в дерево никогда не требует более одного поворота.

Пример 2. Программная реализация основных операций АВЛ-дерева.

#include "stdafx.h"

#include <iostream>

#include <time.h>

using namespace std;

typedef int ElementType;

typedef struct AvlNode *Position;

typedef struct AvlNode *AvlTree;

struct AvlNode {

ElementType Element;

AvlTree Left;

AvlTree Right;

int Height;

};

AvlTree MakeEmpty(AvlTree T);

Position Find(ElementType X, AvlTree T);

Position FindMin(AvlTree T);

Position FindMax(AvlTree T);

AvlTree Insert(ElementType X, AvlTree T);

ElementType Retrieve(Position P);

void printTree(AvlTree T, int l = 0);

int _tmain(int argc, _TCHAR* argv[]){

int i, *a, maxnum;

AvlTree T;

Position P;

int j = 0;

cout << "Введите количество элементов maxnum: ";

cin >> maxnum;

cout << endl;

a = new int[maxnum];

srand(time(NULL)*1000);

// генерация массива

for (i = 0; i < maxnum; i++)

a[i] = rand()%100;

cout << "Вывод сгенерированной последовательности" << endl;

for (i = 0; i < maxnum; i++)

cout << a[i] << " ";

cout << endl;

cout << endl;

// добавление элементов в АВЛ-дерево

T = MakeEmpty(NULL);

for(i = 0; i < maxnum; i++)

T = Insert(a[i], T);

cout << "Вывод АВЛ-дерева" << endl;

printTree(T);

cout << endl;

cout << "Min = " << Retrieve(FindMin(T)) << ", Max = "

<< Retrieve(FindMax(T)) << endl;

// удаление АВЛ-дерева

T = MakeEmpty(T);

delete [] a;

system("pause");

return 0;

}

//функция удаления вершины и его поддеревьев

AvlTree MakeEmpty(AvlTree T) {

if(T!= NULL){

MakeEmpty(T->Left);

MakeEmpty(T->Right);

free(T);

}

return NULL;

}

// поиск вершины со значением X

Position Find(ElementType X, AvlTree T) {

if(T == NULL)

return NULL;

if(X < T->Element)

return Find(X, T->Left);

else

if(X > T->Element)

return Find(X, T->Right);

else

return T;

}

//функция поиска вершины с минимальным значением

Position FindMin(AvlTree T) {

if(T == NULL)

return NULL;

else

if(T->Left == NULL)

return T;

else

return FindMin(T->Left);

}

//функция поиска вершины с максимальным значением

Position FindMax(AvlTree T) {

if(T!= NULL)

while(T->Right!= NULL)

T = T->Right;

return T;

}

//функция возвращает вес вершины

static int Height(Position P) {

if(P == NULL)

return -1;

else

return P->Height;

}

//функция возвращает максимальное из двух чисел

static int Max(int Lhs, int Rhs) {

return Lhs > Rhs? Lhs: Rhs;

}

/*функция выполняет поворот между вершинами K2 и его левым потомком*/

static Position SingleRotateWithLeft(Position K2) {

Position K1;

K1 = K2->Left;

K2->Left = K1->Right;

K1->Right = K2;

K2->Height = Max(Height(K2->Left), Height(K2->Right)) + 1;

K1->Height = Max(Height(K1->Left), K2->Height) + 1;

return K1; //Новый корень

}

//функция выполняет поворот между вершинами K1 и его правым потомком

static Position SingleRotateWithRight(Position K1) {

Position K2;

K2 = K1->Right;

K1->Right = K2->Left;

K2->Left = K1;

K1->Height = Max(Height(K1->Left), Height(K1->Right)) + 1;

K2->Height = Max(Height(K2->Right), K1->Height) + 1;

return K2; //новый корень

}

//функция выполняет двойной левый-правый поворот

static Position DoubleRotateWithLeft(Position K3) {

// поворот между K1 и K2/

K3->Left = SingleRotateWithRight(K3->Left);

// поворот между K3 и K2

return SingleRotateWithLeft(K3);

}

//функция выполняет двойной правый-левый поворот

static Position DoubleRotateWithRight(Position K1) {

// поворот между K3 и K2

K1->Right = SingleRotateWithLeft(K1->Right);

// поворот между K1 и K2

return SingleRotateWithRight(K1);

}

//функция вставки вершины в АВЛ-дерево

AvlTree Insert(ElementType X, AvlTree T){

if(T == NULL){

T = new AvlNode();

if(T == NULL)

fprintf(stderr, "Недостаточно памяти!!!\n");

else {

T->Element = X; T->Height = 0;

T->Left = T->Right = NULL;

}

}

else if(X < T->Element) {

T->Left = Insert(X, T->Left);

if(Height(T->Left) - Height(T->Right) == 2)

if(X < T->Left->Element)

T = SingleRotateWithLeft(T);

else

T = DoubleRotateWithLeft(T);

}

else if(X > T->Element) {

T->Right = Insert(X, T->Right);

if(Height(T->Right) - Height(T->Left) == 2)

if(X > T->Right->Element)

T = SingleRotateWithRight(T);

else

T = DoubleRotateWithRight(T);

}

T->Height = Max(Height(T->Left), Height(T->Right)) + 1;

return T;

}

//функция возвращает значение, хранящееся в вершине

ElementType Retrieve(Position P) {

return P->Element;

}

//функция вывода АВЛ-дерева на печать

void printTree(AvlTree T, int l){

int i;

if (T!= NULL) {

printTree(T->Right, l+1);

for (i=0; i < l; i++) cout << " ";

printf ("%4ld", Retrieve (T));

printTree(T->Left, l+1);

}

else cout << endl;

}

Алгоритм удаления элемента из сбалансированного дерева будет выглядеть так:

Шаг 1. Поиск по дереву.

Шаг 2. Удаление элемента из дерева.

Шаг 3. Восстановление сбалансированности дерева (обратный проход).

Первый шаг необходим, чтобы найти в дереве вершину, которая должна быть удалена. Третий шаг представляет собой обратный проход от места, из которого взят элемент для замены удаляемого, или от места, из которого удален элемент, если в замене не было необходимости. Операция удаления может потребовать перебалансировки всех вершин вдоль обратного пути к корню дерева, т.е. порядка вершин. Таким образом, алгоритмы поиска, добавления и удаления элементов в сбалансированном по АВЛ дереве имеют сложность, пропорциональную .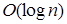

Дата добавления: 2014-01-04