
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Показатели надежности невосстанавливаемых систем
|
|
|
|
ЛЕКЦИЯ 3
Показателями надежности называются количественные характеристики одного или нескольких свойств, составляющих надежность системы. При выборе показателей надежности следует иметь в виду, что эти показатели должны достаточно полно описывать надежностные свойства системы, быть удобными для аналитического расчета и экспериментальной проверки по результатам испытаний, должны иметь разумный физический смысл и, наконец, допускать возможность перехода к показателям эффективности.
Для невосстанавливаёмых систем ограничимся здесь показателями безотказности. Отметим, что эти же показатели описывают системы, в принципе подлежащие восстановлению после отказов, но поведение которых целесообразно рассматривать до момента первого отказа. Кихчислу, например, можно относить системы, чьи отказы чрезвычайно редки и вызывают особо тяжелые последствия.
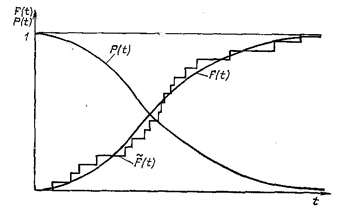
Рис. 1.3 Примерный вид функции распределения F(t) и
функции надежности P(t)
Функция и плотность распределения наработки до отказа. Наработка до отказа Т, как и любая иная случайная величина, описывается функцией распределения F(t), определяемой как вероятность Р случайного события, заключающегося в том, что наработка до отказа Т меньше некоторой заданной наработки t:
F(t)=P { T<t }. (1.1)
Эта вероятность рассматривается как функция t во всем диапазоне возможных значений величины Т.
Функция распределения любой случайной величины является неубывающей функцией времени t. Примерный вид функции F(t) дан на рис. 1.3. Так как значения Т не могут быть отрицательны, то F (0) = 0. При t 
 величина F(t) стремится к единице.
величина F(t) стремится к единице.
Кроме указанного выше вероятностного определения функции F(t), для нее (как и для указанных ниже показателей надежности) можно привести и статистические определения, используемые при испытаниях на надежность. Статистические определения позволяют более полно объяснить смысл вероятностных определений. Чтобы их различать, обозначения статистических определений далее будут отмечать волнистой чертой сверху.
|
|
|
Для рассмотрения статистических определений показателей надежности невосстанавливаемых систем предположим, что на испытания поставлено N одинаковых систем, условия испытаний одинаковы, а испытания каждой из систем проводятся до ее отказа. Обозначим N(t) число систем, отказавших к моменту t, т. е. на интервале (0, t). Очевидно, что N (0) = 0, а при t 
 величина N(t)
величина N(t)  N.
N.
Статистическим определением функции распределения F(t) (или, как говорят, эмпирической функцией распределения) является функция
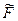 (t)=N(t)/N, (1.2)
(t)=N(t)/N, (1.2)
причем 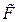 (0) = 0, а при t
(0) = 0, а при t 
 величина
величина 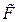 (t)
(t)  1.
1.
График эмпирической функции распределения 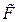 (t) представляет собой ступенчатую линию со скачками, кратными 1/ N в моменты отказов (рис. 1.3).
(t) представляет собой ступенчатую линию со скачками, кратными 1/ N в моменты отказов (рис. 1.3).
Так как события, заключающиеся в наступлении или ненаступлении отказа к моменту t, являются противоположными, то в соответствии с (1.1) введем еще одну функцию
P(t) = P { T 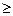 t } = 1 - F(t), (1.3)
t } = 1 - F(t), (1.3)
которую часто называют функцией надежности. Так как при t = 0 система работоспособна, то P (0) = 1. С увеличением времени t P(t) монотонно убывает, а при t 
 величина P (t)
величина P (t) 0. Примерный вид функции P(t) дан на рис. 1.3.
0. Примерный вид функции P(t) дан на рис. 1.3.
Статистическое определение функции надежности следует из (1. 2):
 (t) = 1 -
(t) = 1 -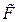 (t) = [N - N(t)]/N, (1.4)
(t) = [N - N(t)]/N, (1.4)
где N-N (t) – число систем, работоспособных к моменту t.
Функция F(t), как правило, непрерывна, и существует непрерывная плотность распределения наработки до отказа
f(t) = dF(t)/dt. (1.5)
Для статистического определения плотности распределения f(t) рассмотрим интервал времени (t - t /2, t+
t /2, t+  t/2), где
t/2), где  t – длина этого интервала. Тогда
t – длина этого интервала. Тогда
 , (1.6)
, (1.6)
где N (t - t /2, t +
t /2, t + t /2) – число систем, отказавших в интервале времени (t -
t /2) – число систем, отказавших в интервале времени (t - t /2, t +
t /2, t + t /2).
t /2).
|
|
|
Вероятности отказа и безотказной работы. Зафиксируем в выражении (1.1) определенное значение t = t 1. Тогда
Q (t 1) = F (t l) = P { T < t 1}, (1.7)
является вероятностью отказа системы до момента t 1.
В отличие от статистического определения функции F (t) во всем диапазоне ее изменения при различных t статистическое определение вероятности отказа 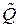 (t 1) на интервале (0, t 1) требует при той же точности оценивания меньших статистических данных. При фиксированном значении t = t 1 статистическое определение вероятности отказа
(t 1) на интервале (0, t 1) требует при той же точности оценивания меньших статистических данных. При фиксированном значении t = t 1 статистическое определение вероятности отказа
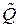 (t 1) = N (t 1) /N. (1.8)
(t 1) = N (t 1) /N. (1.8)
Теперь зафиксируем значение t = t 1 в выражении (1.3). При этом
Р (t 1) = Р { T > t 1}, (1. 9)
называем вероятностью безотказной работы до момента t 1 – вероятностью того, что система проработает безотказно на интервале (0, t 1), начав работать в момент времени t = 0.
Статистическое определение вероятности безотказной работы
 (t 1) = l –
(t 1) = l – 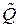 (t 1) = [ N-N (t 1)] / N. (1.10)
(t 1) = [ N-N (t 1)] / N. (1.10)
Для решения различных задач в качестве показателя надежности используется вероятность безотказной работы P(t 1, t 2) системы на интервале (t 1, t 2) при условии, что эта система безотказно проработала до момента t 1. Определим этот показатель по формуле умножения вероятностей, обозначив через А и В соответственно события, выражающие безотказную работу системы на интервалах (0, t 1) и (t 1, t 2). Вероятность события АВ — безотказной работы на интервале (0, t 2) будет
Р { AВ } = Р { A } Р { B/A }.
Отсюда
Р (t 1, t 2) = Р { В/А } = P { АВ } /Р { А } = Р (t 2) /Р (t 1). (1.11)
Интенсивность отказов. При описании надежности невосстанавливаемых систем широкое применение получила такая характеристика, как интенсивность отказов  (t). Она определяется как условная плотность вероятности отказа системы в момент t при условии, что до этого момента отказы не возникали.
(t). Она определяется как условная плотность вероятности отказа системы в момент t при условии, что до этого момента отказы не возникали.
Условная вероятность безотказной работы системы на интервале (t, t+ t) при условии, что система работоспособна в момент t, определяется выражением (1.11):
t) при условии, что система работоспособна в момент t, определяется выражением (1.11):
P (t, t+ t) = P (t+
t) = P (t+ t) /P (t).
t) /P (t).
На интервале (t, t+ t) условная вероятность отказа системы
t) условная вероятность отказа системы
1 – P (t, t+ t) = 1 – P (t, t+
t) = 1 – P (t, t+ t) / P (t) = – [ P (t+
t) / P (t) = – [ P (t+ t) – P (t)] / P (t);
t) – P (t)] / P (t);
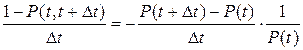 .
.
Устремив  t к нулю, получим
t к нулю, получим
 . (1.12)
. (1.12)
Выражение (1. 12) можно представить в виде
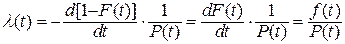 , (1.13)
, (1.13)
из чего следует, что 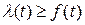 .
.
Решим соотношение (1.12) относительно P (t):
 ,
,
отсюда
P (t) =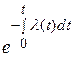 (1.14)
(1.14)
Для статистического определения интенсивности отказов в выражение (1.13) вместо f (t) подставим 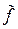 (t) [см. (1.6)], а вместо P (t) подставим
(t) [см. (1.6)], а вместо P (t) подставим  (t) [см. (1.4)], тогда
(t) [см. (1.4)], тогда
|
|
|
 , (1. 15)
, (1. 15)
где N (t- t/ 2, t+
t/ 2, t+ t/ 2) – число систем, отказавших на интервале (t–
t/ 2) – число систем, отказавших на интервале (t– t/ 2, t+
t/ 2, t+ t/ 2);
t/ 2);
N - N (t) – число систем, работоспособных к моменту t.
Так как функции F (t) и P (t) безразмерны, то размерность интенсивности отказов, как это следует из (1.13) – величина, обратная наработке t (например, 1/ч).
Интенсивность отказов  (t) дает наглядную картину изменения безотказности. Типичная зависимость
(t) дает наглядную картину изменения безотказности. Типичная зависимость  (t) во времени дана на рис. 1.4. Ниспадающий вид кривой
(t) во времени дана на рис. 1.4. Ниспадающий вид кривой  (t) относится к периоду приработки системы (1-й участок). При этом выявляются скрытые дефекты изготовления отдельных элементов системы, недостатки монтажа, наладки, нарушения, произошедшие в результате транспортировки. По окончании приработки наступает период нормальной эксплуатации (2-й участок). В течение этого времени интенсивность отказов относительно неизменна. Именно этот участок соответствует основному времени эксплуатации систем. Возрастание кривой
(t) относится к периоду приработки системы (1-й участок). При этом выявляются скрытые дефекты изготовления отдельных элементов системы, недостатки монтажа, наладки, нарушения, произошедшие в результате транспортировки. По окончании приработки наступает период нормальной эксплуатации (2-й участок). В течение этого времени интенсивность отказов относительно неизменна. Именно этот участок соответствует основному времени эксплуатации систем. Возрастание кривой  (t) относится к периоду старения системы из-за износа отдельных ее элементов и изменения их характеристик (3-й участок).
(t) относится к периоду старения системы из-за износа отдельных ее элементов и изменения их характеристик (3-й участок).

Рис. 1.4 График изменения интенсивности отказов
Средняя наработка до отказа. Функции F (t), f(t), P (t),  (t) полностью описывают случайную величину Т. В то же время для решения значительного числа задач надежности достаточно знать только показатели, являющиеся числовыми характеристиками этой случайной величины. К ним в первую очередь относится средняя наработка до отказа (среднее время безотказной работы) – математическое ожидание случайной величины Т – наработки до отказа (или времени безотказной работы)
(t) полностью описывают случайную величину Т. В то же время для решения значительного числа задач надежности достаточно знать только показатели, являющиеся числовыми характеристиками этой случайной величины. К ним в первую очередь относится средняя наработка до отказа (среднее время безотказной работы) – математическое ожидание случайной величины Т – наработки до отказа (или времени безотказной работы)
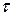 = М [ T ] =
= М [ T ] =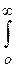 tf (t) dt, (1. 16)
tf (t) dt, (1. 16)
где М – символ математического ожидания.
Преобразуем выражение (1.16) к виду
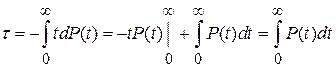 . (1.17)
. (1.17)
Отсюда следует, что средняя наработка до отказа геометрически равнаплощади под кривой P (t) (см. рис. 1.4).
Статистическое определение средней наработки до отказа
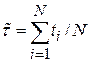 , (1.18)
, (1.18)
где ti – наработка до отказа i -й системы; N – число систем.
Реже используются такие показатели, как дисперсия и среднеквадратическое отклонение наработки до отказа:
|
|
|
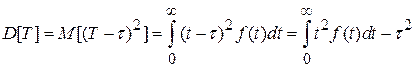 ; (1.19)
; (1.19)

где 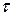 т и
т и 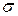 [ Т ] имеют размерность времени (обычно они выражаются в часах); D [ Т ] – квадрата времени.
[ Т ] имеют размерность времени (обычно они выражаются в часах); D [ Т ] – квадрата времени.
Статистические определения дисперсии и среднеквадратического отклонения соответственно

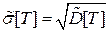 . (1.20)
. (1.20)
Взаимосвязь показателей безотказности невосстанавливаемых систем показана в табл. 1.1. Знание любой функции F (t), Р (t), f (t),  (t) дает возможность найти три остальные.
(t) дает возможность найти три остальные.
Таблица 1.1
| Характе-ристики | F (t) | P (t) | 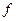 (t) (t)
| 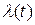
|
| Функция распреде-ления наработки до отказа | – | 1- P (t) | 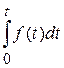
| 
|
| Функция надёжно-сти Р (t) | 1- F (t) | – | 1-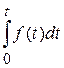 =
= =
=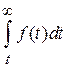
| 
|
Плотность распреде-ления 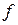 (t) (t)
| 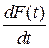
| – 
| – | 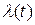 
|
Интенсив-ность отказов 
|  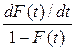
| –
| 
| – |
Средняя наработка до отказа 
| 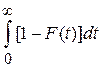
| 
| 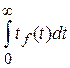
| 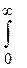 
|
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 1234; Нарушение авторских прав?; Мы поможем в написании вашей работы!