Послідовне з’єднання елементів

Розглянемо коло (рис. 2.18, а), в якому n резисторів, n індуктивностей та n ємностей, з’єднані між собою послідовно і підключені до джерела синусоїдної напруги.

За другим законом Кірхгофа, рівняння у миттєвих значеннях напруг кола має вигляд:

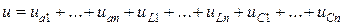
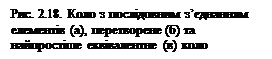
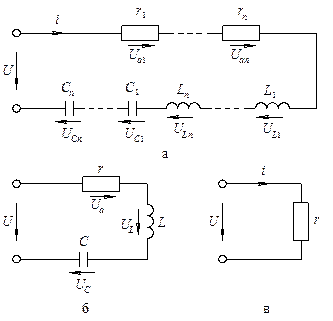
Враховуючи, що при послідовному з’єднанні спільним для всіх ділянок кола є струм, то прийнявши початкову фазу синусоїди струму y _i = 0^°, рівняння струму і напруги кола запишемо так:

,

.

За таких умов рівняння, записане за другим законом Кірхгофа матиме вигляд –

або:

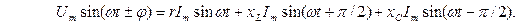
Звідси випливає, що вихідне коло може бути перетворено і надано у вигляді, як на рис. 2.18, б, де

; ; .

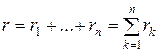Отже, при послідовному з’єднанні n резисторів, або n індуктивностей, результуючий активний опір та результуюча індуктивність кола, дорівнюють, відповідно, сумам активних опорів і індуктивностей ділянок цього кола. З іншого боку, при послідовному з’єднанні n ємностей, результуюча ємність кола буде менше найменшої ємності будь-якої ділянки цього кола.

При w t = p/2 і w t = 0 рівняння миттєвих значень напруг кола зводиться до рівностей:

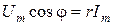та .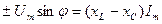

Піднесемо до квадрату перше та друге з цих рівностей та додамо їх. Використавши, що , одержимо:

.

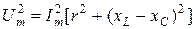Поділивши ліву і праву частини одержаного рівняння на 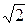, після виконання перетворень, одержимо рівняння, яке описує зв’язок між струмом і напругою, тобто закон Ома для кола з послідовним з’єднанням r, L, C елементів:

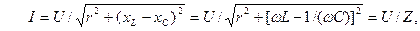
де 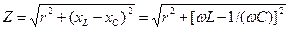– повний опір кола, Ом.

З викладеного випливає, що вихідне (рис. 2.18, а) і перетворене (там же, б) кола можуть бути зведені до найпростішого еквівалентного, як на рис. 2.18, в.

У комплексній формі для кола з послідовним з’єднанням r, L, C, маємо:

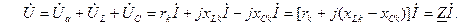
Звідси рівняння закону Ома у комплексній формі буде:

.

Тут Z – комплекс повного опору кола, що дорівнює:

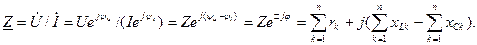
У загальному випадку комплекс повного опору кола може бути розрахований, як сума комплексів повних опорів включених послідовно ділянок кола:

.

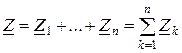Векторна діаграма вихідного (рис. 2.18, а) і перетвореного (рис. 2.18, б) кола, що наведена на рис. 2.19, а (при побудові умовно прийнято U_C > U_L) може бути зведена до прямокутного трикутника напруг (рис. 2.19, б). У цьому трикутнику, один з катетів є пропорційним спаду напруги 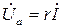на еквівалентному активному опорі кола, другий – спаду напругина еквівалентному реактивному опорі кола, а гіпотенуза – спаду напруги на повному опорі кола.

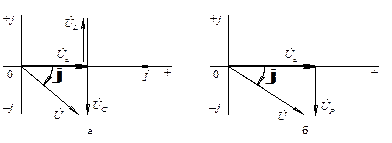
В результаті ділення кожної із сторін трикутника напруг на струм кола отримуємо трикутник опорів (рис. 2.20, а). У цьому прямокутному трикутнику, один з катетів є пропорційним еквівалентному активному r опору кола, другий – еквівалентному реактивному jx = j (x_L - x_С) опору, а гіпотенуза – повному опорі Z кола.

Для трикутника напруг і трикутника опорів, на підставі теореми Піфагора та тригонометричних співвідношень, маємо:

,

,

,

.

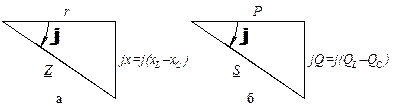
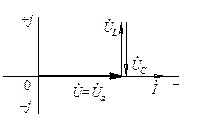
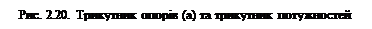
В результаті множення кожної зі сторін трикутника напруг на струм кола отримуємо трикутник потужностей (рис. 2.20, б). У цьому прямокутному трикутнику, один з катетів є пропорційним активній потужності Р кола, другий – реактивній потужності jQ = j (Q_L - Q_С) кола, а гіпотенуза – повній потужності S кола.

З аналізу трикутника потужностей випливає, що при послідовному з’єднанні опорів активну і реактивну потужності кола синусоїдного струму можна визначати як суми відповідних потужностей k ділянок кола:

,

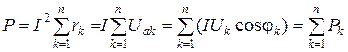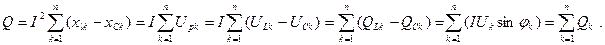
При цьому повна потужність кола не є алгебраїчною сумою повних потужностей ділянок цього кола:

.

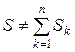Її значення може бути розраховане через її складові так:

,

або ж:

.

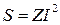Звернемо увагу, що у трикутнику потужностей, так як і в трикутниках напруг і опорів, кут зсуву фаз j між струмом і напругою кола розташований між активною складовою і повною величиною. Отже, з трикутника потужностей маємо:

,

.

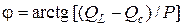На практиці, активна потужність Р є пропорційною обсягу продукції, яку виробляють за рахунок споживання з мережі потужності S. Тому cosj часто називають коефіцієнтом використання електричної потужності.

Комплекс повної потужності послідовного кола розраховують так:

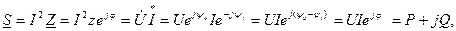
де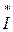– спряжений комплекс струму кола.

У записах комплексу повної потужності, а також повного опору кола, знак перед j визначає характер навантаження цього кола. Так, при j > 0 – коло має активно-індуктивний характер навантаження, а при j < 0 – активно-ємнісний.

Якщо для кола, яке містить з’єднані послідовно r, L, C елементи, j = 0^°, то у такому колі має місце так званий резонанс напруг. Умовою настання цього явища рівність реактивних опорів кола

,

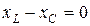тобто:

2p fL = 1/(2p fC).

При резонансі напруг векторна діаграма кола має вигляд, як на рис. 1.22. Важливою ознакою резонансу напруг є максимально можливий для даного кола струм. В умовах резонансу, при x_L = x_С >> r, спади напруг на ділянках з індуктивними і ємнісними елементами за своїми значеннями можуть набагато перебільшувати вхідну напругу кола U_L = U_С >> U. Таке підвищення напруги може призвести до пробою ізоляції і, як наслідок, настання аварійного режиму короткого замикання. Тому, явище резонансу напруг є вкрай небажаним для електрообладнання і небезпечним для обслуговуючого персоналу. Разом з тим, його широко використовують в радіотехніці.

Дата добавления: 2014-01-04