Метод анализа размерностей

52.

Ду

Др

УЬ

/

Цх.У)

Г77777777777777П,

>' *-------------------------------------- >■

77777777777777"

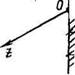
Рис. 2.22. Поле температуры и поле скорости при движении жидкости вдоль плоской

поверхности

В результате теплового и динамического взаимодействия стенки с потоком температура и скорость последнего в пристенной области меняются. Формируются поле температуры 1(х, у) и поле скорости м?(х, у). В направлении оси 2 по условию задачи никаких изменений не происходит. Рассматриваемый процесс является стационарным.

Для данного случая запишем систему дифференциальных уравнений конвективного теплообмена - уравнения энергии, движения и сплошности; из уравнений исключаются члены, связанные с изменением величин во времени и по оси 2. Уравнение энергии будет иметь следующий вид:

рС,

(

И\

дх

+ м>.

= Х

•+•

(д²* а²/

дх* ду<

(2.74)

Две проекции уравнения движения на оси ЛГи Г могут быть представлены следующим образом:

дщ дх ди>

И\

УУ*

•'+ и\

д^] ду

_у дн>_у^л

ду

дх

=рё

^х дх

V

+ р

' д²м?_г д²м>_г

дх'

ду<

^гд\ -д'пу

V

--- г- + -

дх'

(2.75)

(2.76)

Уравнения (2.75) и (2.76) называют еще уравнениями Навье-Стокса в честь известных ученых, слагаемые этих уравнений имеют размерность силы, отнесенной к единице объема.

Уравнение сплошности или неразрыности для несжимаемой жидкости (р = сопзг) имеет
следующий вид: ■

дм>_г 'дю*

•■■+■•

= 0

дх ду Уравнение (2.77) является уравнением сохранения массы.

(2.77)

В уравнениях (2.74) - (2.77) щ, м>_у - проекции вектора скорости на оси X и У; §_х, $у ~ проекции вектора ускорения свободного падения на осиХи У;др - изменение давления.

Для описания рассматриваемого процесса конвективного теплообмена к уравнениям необходимо добавить условия однозначности. Пространственная область, в которой рассматривается процесс конвективного теплообмена задана следующими геометрическими условиями:

0<л:</₀; 0<у<+оо; -оо<2<+оо. (2.78)

Поскольку процесс стационарен, начальные условия отпадают. Граничные условия для искомых функций /, щ, м>_уир могут быть заданы следующим образом:

• на поверхности стенки при у = 0, 0 <. х < /₀

{ = {_с;м>_х=ч>_у=0;. (2.79)

• на бесконечном удалении от стенки при у -> +оо, 0 < х < /₀

'*(*> ™_Х*Щ\ иу*0 • (2.80)

Давление р следует задать в начальном сечении при х = 0, 0<у< +оо.

Уравнения (2.74) - (2.77) совместно с условиями однозначности (2.78) - (2.80) описывают процесс конвективного теплообмена на плоскости. Для потока сжимаемой жидкости, движущейся в трехмерном пространстве при нестационарном режиме, уравнения (2.74) - (2.77) должны быть дополнены.

Уравнение энергии, устанавливающее связь между пространственным и временным изменением температуры в любой точке движущейся жидкости, можно записать в следующем виде:

— +-\» — + и» — + м>₂— = а7{- (2.81)

дт дх ду дг

Если щ • \\>_у - м>₂ ^в 0, то уравнение (2.81) превращается в дифференциальное уравнение теплопроводности для твердого тела.

Для компактной записи уравнение движения удобно представить в векторной форме

р~ = Р2-Ур + /иУ²™> (²-⁸²)

ще величина й?й7 / с1т - характеризует изменение скорости во времени.

Уравнение (2.82) составлено без учета зависимости физических параметров жидкости >т температуры.

Уравнение неразрывности для потока сжимаемой жидкости (р Ф сопзт) примет вид

' ^ ₊ ^^ ₊:^ ₊ ^1) ₌ о. (2.83)

дт дх ду дг

Уравнения (2.81)-(2.83) описывают множество процессов конвективного гплообмена, чтобы выделить какой-то конкретный процесс, к этим уравнениям необходимо обавить условия однозначности (геометрические, физические, начальные и граничные).

Система дифференциальных уравнений (2.81) - (2.83) в совокупности с условиями цнозначности представляет собой математическую формулировку задачи конвективного гплообмена.

2.3.5. Основы теории подобия

2.3.5.1. Три вида подобия

Конвективный теплообмен описывается системой дифференциальных уравнений и условиями однозначности, которые содержат большое количество неизвестных. Аналитическое решение полной системы дифференциальных уравнений очень трудоемко, поэтому при решении задач конвективного теплообмена большое значение приобретает экспериментальный путь исследований.

Недостатком экспериментальных исследований является невозможность распространения результатов, полученных в данном опыте, на другие явления и процессы, отличающиеся от изученного. Теория подобия объединяет методы теоретических и экспериментальных исследований, ее развитие связано с необходимостью постановки модельных экспериментов. Теория подобия позволяет сделать ряд выводов из дифференциальных уравнений и условий однозначности, не прибегая к интегрированию, и тем самым обосновать теоретическую базу для постановки опытов и обработки экспериментальных данных.

С помощью теории подобия размерные физические величины объединяют в безразмерные комплексы, число которых значительно меньше, чем неизвестных величин. Безразмерные комплексы рассматриваются как новые переменные, что упрощает исследование физических процессов.

Теория подобия устанавливает такие условия, при которых результаты экспериментальных исследований можно распространить на другие явления, подобные рассматриваемому.

Различают три вида подобия:

1. Геометрическое подобие - подобие углов, линейных размеров, геометрических фигур и т. д.

2. Кинематическое подобие - подобие распределения скоростей в сходственных точках.

3. Полное подобие физических явлений - этот вид подобия означает, что все величины, характеризующие данные явления, должны находиться в определенных соотношениях для сходственных точек и сходственных моментов времени.

Подобными могут быть лишь явления одного и того же класса, т. е. явления, которые описываются одним и тем же дифференциальным уравнением. Подобие двух физических явлений означает подобие всех величин, характеризующих рассматриваемое явление. Это означает, что в сходственных точках пространства в сходственные моменты времени любая величина ■</>' одного процесса пропорциональна однородной ей величине другого процесса <р"

... //>" = С,,.<, (2.84)

где С(р - коэффициент пропорциональности, называемый константой подобия. Константа подобия не зависит ни от координат, ни от времени.

2.3.5.2. Критерии подобия

Подобие двух явлений рассмотрим на примере равномерного прямолинейного движения двух потоков жидкости. Первый поток движется со скоростью м>' (см. рис. 2.23 а), а второй со скоростью м>* (см. рис. 2.23 б).

-> М>') 1 •------ > V

Рис. 2.23. Прямолинейное движение двух потоков жидкости в трубах

Скорость можно выразить через длину пути и время:

• для случая на рис. 2.23 а и»' = VI г';

• для случая на рис. 2.23 б м>" = VI г".

Для скоростей м^и ^"справедливо следующее соотношение

±±ЖМ±. (2.85)

V' т7 г" VI г"

Полученную пропорцию можно переписать, используя константы подобия

С„ = С, 1С_Х или С„С_Т IС₁ = 1. (2.86)

Из последнего соотношения видно, что для подобия двух явлений необходимо, чтобы безразмерный комплекс, составленный из констант подобия, был равен 1. Заменив значения констант подобия в последнем уравнении на размерные физические величины, получим

м/т' >/г"

/' /"

я Шт ■ (2.87)

Таким образом, существуют величины, которые для всех подобных между собой явлений сохраняют одно и то же числовое значение. Такие комплексы величин называют критериями подобия, или инвариантами.

Критерий подобия - это безразмерное соотношение параметров, характеризующих процесс, которое у подобных явлений в сходственных точках в сходственные моменты времени имеет численно одинаковое значение.

Критерии подобия принято назвать именами крупных ученых, известных своими работами в области тепломассообмена и гидродинамики, и обозначать двумя буквами, например, Ке - критерий Рейнольдса, Ео - критерий Фурье и другие. Возможно также обозначение некоторых критериев заглавными русскими буквами с индексом, например, К},

К₂,КзИТ.Д. ■::-,...,. •■ ц>

Для решения задач конвективного теплообмена наиболее часто используются следующие критерии подобия.

1. Критерий Рейнольдса Ке - определяет режим движения жидкости и выражает соотношение между силой инерции и силой внутреннего трения (вязкости), определяется по формуле (2.68).

2. Критерий Нусселъта Ыи - характеризует теплообмен на границе жидкость-стенка

Ш = ~, (2.88)

X

где а - коэффициент теплоотдачи, Вт/^-К); / - характерный линейный размер, м; Х_ж -коэффициент теплопроводности жидкости, Вт/(м-К).

3. Критерий Пекле Ре - выражает соотношение между двумя видами теплообмена:
теплопроводностью и конвекцией

Ре = ~, (2.89)

а

где м> - скорость потока жидкости, м/с; а - коэффициент температуропроводности, м²/с.

4. Критерий Прандтля Рг - характеризует физические свойства жидкости

Рг = у/а, - (2.90)

где V - кинематический коэффициент вязкости, м²/с.

Критерий Прандля можно выразить через два других критерия Ре и Яе: Рг = Ре /Ке.

5. Критерий Грасгофа Ог - характеризует свободную конвекцию и выражает
соотношение между подъемными силами, возникающими в жидкости при нагреве, и силами
вязкости

О-*^*. (2.91)

V

где # - ускорение свободного падения, м/с; Ах - разность температур между жидкостью и поверхностью, °С; /? - коэффициент объемного расширения (показывающий, на какую часть первоначального объема произошло расширение при А( =1), 1/°С.

6. Критерий Фурье Ро - характеризует нестационарность процессов

Ро^~, (2.92)

где а - коэффициент температуропроводности, м²/с; г - время, с.

2.3.5.3. Теоремы подобия

Практическое применение теории подобия базируется на трех теоремах. Две первые из них говорят о явлениях, подобие которых заранее известно, и формулируют основные свойства подобньк между собой явлений. Третья теорема обратная первым двум, она устанавливает признаки, по которым можно узнать, подобны ли два явления друг другу. В этом параграфе рассматриваются только формулировки теорем подобия, подробные доказательства приводятся в учебнике [2].

1. Теорема Ньютона. Первая теорема подобия для подобного течения двух жидкостей
была высказана И. Ньютоном в 1686 г. Однако строгое доказательство теоремы было дано
Ж. Бертраном в 1848 г. Формулировка теоремы Ньютона: подобные между собой явления
имеют численно одинаковые критерии подобия (Ке = Ыет, Ыи = Мет).

Первая теорема подобия устанавливает связь между константами подобия и позволяет вывести уравнения для чисел подобия. Теорема указывает, что при выполнении опытов необходимо и достаточно измерять лишь те величины, которые входят в числа подобия изучаемого явления.

2. Теорема Букингема. Вторая теорема подобия была доказана в 1911 г. русским
ученым А. Федёрманом и в 1914 г. американским ученым Е. Букингемом. Формулировка
теоремы Букингема: любая зависимость между переменными, характеризующими какое-
либо явление, может быть представлена в виде зависимости между критериями подобия.

Из второй теоремы подобия следует, что если результаты любого экперимента обработать в числах подобия, то зависимость между ними необходимо выражать в виде уравнения подобия, которое может быть записано в виде

ДК₁,К₂,К₃,...,К_п) = 0 (2.93)

Зависимость (2.93) называют обобщенным критериальным уравнением. Это уравнение любую зависимость между величинами, характеризующими данное явление, представляет зависимостью между числами подобия. Для всех подобных явлений критериальные зависимости одинаковы.

3. Теорема Кирпичева - Гухмана. Третья теорема подобия устанавливает необходимые условия для того, чтобы явления оказались подобными друг другу. Формулировка ее была дана М. В. Кирпичевым и А. А. Гухманом, а доказательство теоремы - М. В. Кирпичевым в 1933 г. Формулировка теоремы: подобны те явления, условия однозначности которых подобны, и критерии подобия, составленные из условий однозначности, численно одинаковы.

Теоремы подобия и теория подобия в целом дают общие методические указания, как поступить в каждом отдельном случае при анализе уравнений, описывающих явление, устанавливают пути для правильной постановки опыта и дают указания по обработке полученных результатов. Теория подобия устанавливает также условия, при которых результаты экспериментальных исследований можно распространить на другие явления, подобные рассматриваемому. В итоге можно отметить, что теория подобия является научной основой проведения экспериментов по изучению процессов тепломассообмена и обобщения результатов опытов.

I

2.3.5.4. Критериальное уравнение конвективного теплообмена

в общем виде

Критериальным уравнением называют зависимость между каким-либо определяемым критерием подобия и другими определяющими критериями подобия.

Определяемыми критериями подобия являются критерии, в которые входят искомые зависимые переменные, а определяющими - критерии, целиком составленные из независимых переменных и постоянных величин, входящих в условия однозначности. В зависимости от постановки задачи определяющие критерии могут становиться определяемыми.

При решении задач конвективного теплообмена неизвестной величиной чаще всего является коэффициент теплоотдачи а, Вт/(м²-К), поэтому определяемым критерием является критерий Нуссельта Ыи.

Для нестационарных процессов критериальное уравнение конвективного теплообмена
может быть представлено в общем виде.:

№ = /(Рд, Ке, Рг, Ог). (2.94)

В случае стационарного процесса из зависимости (2.94) исчезнет критерий Ро, и критериальное уравнение конвективного теплообмена примет вид

Ш = А-Ке"Рг^твг^к, (2.95)

где А, п, т, #- постоянные величины, зависящие от конкретных условий.

Схема решения задач конвективного теплообмена заключается в следующем: с помощью критериальных уравнений ищется значение критерия Ыи. Найденное значение Ыи подставляется в формулу (2.88), из которой находится неизвестный коэффициент теплоотдачи

а = ^^-. (2.96)

I

Таким образом, значение коэффициента а будет зависеть от правильного выбора критериального уравнения для расчета критерия Нуссельта. Критериальные уравнения для наиболее часто встречающихся случаев конвективного теплообмена представлены в параграфе 2.4. настоящего пособия.

Необходимой предпосылкой теории подобия является математическое описание изучаемого процесса в виде дифференциальных уравнений и условий однозначности. Из математической формулировки задачи следует перечень существенных для рассматриваемого процесса физических величин. Если перечень установлен, то выявление критериев подобия может быть произведено методом анализа размерностей.

Иногда список безразмерных величин устанавливают интуитивно, без строгой формулировки краевой задачи. В этом случае возможны ошибки. Во избежание ошибок при выборе критериев подобия предложен метод анализа размерностей.

Подробно метод анализа размерностей рассматривается в специальной литературе. Мы ограничимся рассмотрением некоторых выводов, следующих из анализа размерностей и имеющих интерес для практического использования обобщенных переменных.

Можно различать два вида физических величин: первичные (основные) и вторичные (производные).

Первичные величины характеризуют какое-либо физическое явление непосредственно, без связи с другими величинами.

Вторичными являются величины, которые выражаются через первичные согласно определениям или физическим законам. Так, например, если длина и время являются первичными величинами, т. е. если длину нельзя выразить через время (и наоборот), то скорость, представляющая собой по определению отношение длины ко времени, является вторичной, производной величиной.

Выбор первичных величин, вообще говоря, произволен. В еиетеме СИ за первичные выбраны длина Ь, масса А/, время Т, температура 0, сила тока 7, сила света 1 Известны и другие системы первичных величин, используемых или предложенных к использованию. Например, Гауссом было предложено использовать в качестве первичных величин длину, массу и время; остальные мыслимые величины должны быть производными. При выборе первичных величин большое значение имеет вопрос об удобстве их применения.

Символическое выражение производной величины через основные (первичные) называется размерностью, О размерности можно говорить только применительно к определенной системе первичных величин. Размерность можно представить в виде степенной формулы. Применительно к системе СИ формула размерности имеет вид

[(р] = 1^щМ^П2Т^щ0^пЧ^пЧ^ч, (2.97)

где [у] - производная единица измерения; щ - действительные числа.

Размерность вторичной величины относительно данной первичной / может быть
охарактеризована значением показателя степени щ при этой первичной величине. Поэтому
безразмерные числа часто называют величинами с нулевой размерностью, так как для них
все показатели степени в формуле размерности (2.97) равны нулю. Согласно формуле (2.97)
размерность первичной величины можно принять равной единице (берется относительно
себя).' •!

Помимо размерности физические величины характеризуются числовыми значениями. Числовые значения первичных величин получают путем прямого измерения, т. е. путем сопоставления измеряемой величины с некоторой величиной той же физической природы, выбранной в качестве стандарта и называемой единицей физической величины. Выбор единиц первичных величин (основных) произволен и определяется вопросами удобства их использования.

Числовое значение вторичной величины определяется косвенным путем, его находят по числовым значениям первичных величин. От выбора единиц первичных величин зависят

численные значения как первичных, так и вторичных величин. От выбора основных единиц * физических величин не зависят только численные значения безразмерных величин (величин

с нулевой размерностью).
' Выбор перечня первичных величин и их единиц является необходимым и основным

■ шагом на пути создания системы единиц физических величин.

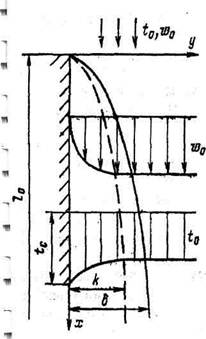
Рассмотрим пример использования метода размерностей. Определим безразмерные

переменные для случая, когда поверхность твердого тела омывается несжимаемой

⁴ жидкостью при стационарном режиме. Температура и скорость вдали от тела постоянны и

равны соответственно?о и м>о- Размер тела /о задан. Температура поверхности тела равна 1_С,

причем {с>1о-

Расположим оси координат так, как показано на рис. 2.24. Для простоты примем, что - ось У нормальна к поверхности тела, а ось X направлена вдоль тела вертикально, при этом „ 2х ⁼ ё> а проекции вектора силы тяжести на оси Ги 2§_у =&= 0.

Размер тела вдоль оси 2 намного больше /о. Введем обозначение избыточной I температуры в = I - Г₀, где I - температура жидкости. Заметим, что Л = Ш, т. к. /₀ = сопз*.

Будем полагать, что физические параметры жидкости также постоянны. Учтем только подъемную силу, возникающую в результате зависимости плотности от температуры. Подъемная сила р^рв будет соизмерима с вязкостным членом ц(д²м>_х1ду²) дифференциального уравнения движения. (.

При принятых условиях поля температур и скоростей можно описать следующими дифференциальными уравнениями:

уравнение энергии:

	дв	дв	д^2в
Чх	— +-И'	------	-а —г->
	дх ^у	ду	V

уравнение движения:

д% ду²

дм>

дм?_г

(2.99)

м>_г

•+Ж

(2.98)

X _.

+ &6\

Рис. 2.24. Течение несжимаемой жидкости около твердой стенки

дх ^у ду уравнение сплошности: ди>„ дм/.

= 0.

(2.100)

дх ду Граничные условия запишем в виде:

• вдалиоттелаО = оо):0 = 0_о=О; Щ~Щ1 м_у=0; ₍ < л;>.„• _;

• на поверхности тела (у = 0, 0 < х < 1₀,. -оо < г < +<ю): в = в_с '* (_с - 1₀ - сопз!;

Из математической формулировки этой задачи следует, что

0= /(х,у,в_с,1₀,щ,у,а,8Р).

(2.101)

В списке величин, существенных для рассматриваемого процесса, представлено девять ^временных (л = 9). В рассматриваемом нами примере использованы три первичные величины системы единиц СИ: длина, время, температура (к = 3).

- _? Пользуясь возможностью произвольного выбора основных единиц, разделим переменные, входящие в уравнение (2.101), на две группы: на величины с независимой

Дата добавления: 2014-01-04