Галопирующие колебания вагона

Галопирующие колебания – это вращательные колебания вокруг горизонтальной оси Y, перпендикулярной бортам вагона и проходящей через центр масс вагона. При этом движение вагона подобно галопу лошади. Колебания обусловлены упругими силами подвески и инертностью вагона.

Пусть из-за случайного толчка, например на стыке рельсов или при падении груза, корпус вагона наклонился. Пусть при этом пружины передней вагонной тележки сжались, а задней тележки – растянулись. Возникает момент упругих сил пружин подвески, стремящийся вернуть вагон в положение равновесия. Но вагон по инерции проходит положение равновесия, поворачиваясь в противоположном направлении. Потом движение повторяется в обратном направлении, и таким образом возникают галопирующие колебания.

Определим период галопирующих колебаний. Так как это вращательные колебания, то для вывода применим основной закон динамики вращательного движения: произведение момента инерции вагона относительно оси вращения на угловое ускорение равно моменту упругих сил подвески: J ε = М.

Получим формулу для момента силы, который создают пружины подвески. По закону Гука упругие силы пружин пропорциональны деформации пружин и направлены противоположно деформации F = –kx. Так как передняя подвеска сжата, то ее сила упругости направлена вертикально вверх, а сила упругости растянутой задней подвески – вниз (рис. 14.4). Момент пары упругих сил подвески F равен произведению силы на плечо пары сил: M = F l, где плечо l равно расстоянию между линиями действия сил, то есть между серединами передней и задней вагонных тележек. Деформация пружин х связана с углом поворота вагона как длина дуги с центральным углом: 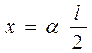. Итак, момент упругих сил, действующий на вагон, равен

.

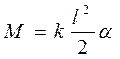Подставив в закон динамики вращательного движения формулу момента силы, получим дифференциальное уравнение галопирующих колебаний 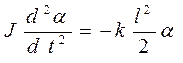. (14.14)

Здесь угловое ускорение записано как вторая производная от угла поворота по времени. Решением этого дифференциального уравнения должна быть функция, у которой вторая производная имеет такой же вид, как и сама функция, но противоположного знака. Например, это может быть функция косинуса

α= α ₀ cos ω t, (14.15)

где α ₀ – амплитуда колебаний, ω – циклическая частота колебаний. Если определить вторую производную от угла поворота по времени 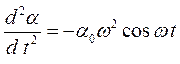и подставить в дифференциальное уравнение, то выбранная функция будет решением, при условии, если циклическая частота колебаний равна 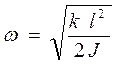. Период колебаний 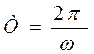будет равен

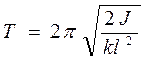. (14.16)

Здесь k –– коэффициент упругости пружин подвески, принятый одинаковым для передней и задней вагонных тележек, J – момент инерции вагона.

Дата добавления: 2014-01-04