Поле бесконечной заряженной нити

Рассмотрим поле, созданное зарядом, равномерно распределенным по бесконечной нити. Эту задачу мы решили на прошлой лекции, воспользовавшись принципом суперпозиции электрических полей (см. 1.11).

Теперь покажем, несколько проще можно рассчитать это поле с помощью теоремы Гаусса.

Определим напряжённость поля на расстоянии r от нити, заряженной с постоянной линейной плотностью :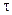

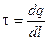, [Кл/м] (2.10)

Окружим нить замкнутой цилиндрической поверхностью (рис. 2.7.). Высота цилиндра — h, а радиус его основания — r.

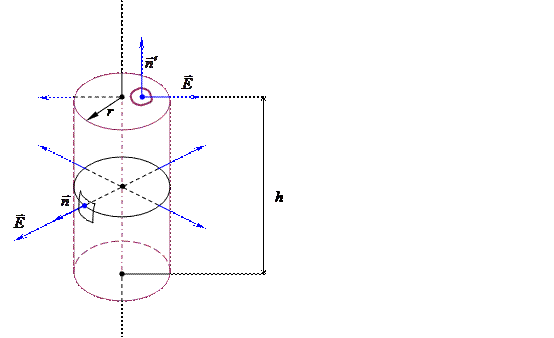
Рис. 2.7.

Поле, созданное заряженной нитью, обладает цилиндрической симметрией. В связи с этим векторы напряжённости во всех точках боковой поверхности цилиндра будут одинаковы по модулю и направлены радиально, то есть перпендикулярно к боковой поверхности цилиндра. На основаниях цилиндра векторы 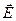, направленные по-прежнему радиально, «скользят» по основанию, образуя прямой угол с нормалью .

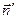Вычислим поток вектора 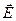через поверхность выбранного цилиндра. Полный поток через эту замкнутую «гауссову» поверхность складывается из потока через боковую поверхность цилиндра и через два его основания:

Последние два интеграла равны нулю, так как «скользящие» по основаниям цилиндра векторы 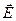не пронизывают их и не создают никакого потока. Формально эти два интеграла равны нулю, так как между векторам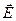и и 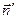прямой угол и 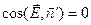. Таким образом

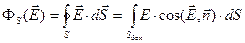
Во всех точках боковой поверхности цилиндра E = Е_r = const и .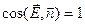

Поэтому поток через боковую поверхность цилиндра равен

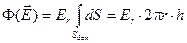(2.11)

Это поток вектора напряжённости электрического поля, вычисленный по определению потока.

Теперь воспользуемся теоремой Гаусса, отметив предварительно, что «заряд, заключённый внутри гауссовой поверхности» в данном случае сосредоточен на отрезке нити h — на оси цилиндра:

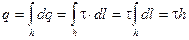
Таким образом

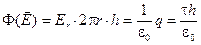(2.12)

Отсюда теперь легко получить знакомую нам гиперболическую зависимость напряжённости поля от расстояния до нити — r (см. 1.11).

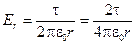(2.13)

Дата добавления: 2014-01-04