Метод Д’Аламбера (для розв’язування задачі про вільні поперечні коливання нескінченої струни)

Поперечні коливання нескінченної струни

Лекція 4 Методи розв’язування задач про коливання струни

Перш ніж розв’язувати задачу про коливання закріпленої струни, розглянемо більш просту задачу про коливання нескінченної струни.

Розглянемо вільні поперечні коливання нескінченної струни в наступній постановці:

,

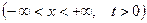П.У. 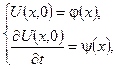(4.1)

де функці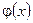ї і 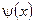задані на всій числовій осі.

Задача полягає у знаходженні функції , яка визначає переміщення будь-якої точки х у будь-який момент часу t. По-перше, зведемо хвильове рівняння до канонічного виду. Це рівняння гіперболічного типу. Оскільки визначник

Згідно з методом характеристик запишемо рівняння:

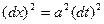або .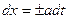

Отже, отримали два звичайних диференціальних рівняння. Проінтегруємо кожне з них:

1)

2)

Тепер введемо нові змінні: .

Щоб у хвильовому рівнянні перейти до цих змінних, знайдемо відповідні частинні похідні та 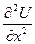, врахувавши, що

;; ;

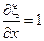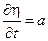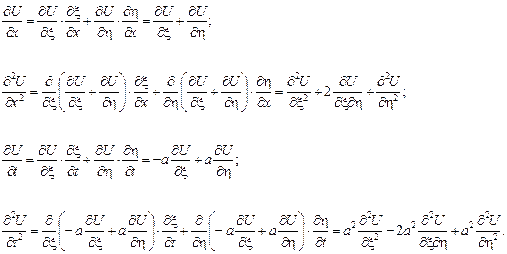
Підставивши ці похідні у хвильове рівняння, отримаємо:

Звідси 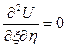– це хвильове рівняння у канонічному виді. Проінтегрувавши його спочатку по , потім по , отримаємо розв’язок:

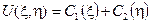, або:

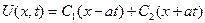. (4.2)

Це загальний розв’язок хвильового рівняння, де 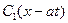та довільні двічі диференційовні функції. Щоб їх знайти, використаємо початкові умови:

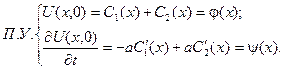
Після інтегрування другого рівняння у межах від 0 до , отримаємо систему:

де

Розв’язавши систему рівнянь, знайдемо шукані функції:

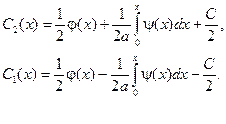
Щоб отримати функції 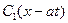та 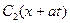, достатньо замість аргумента х підставити відповідні аргументи та . Отже, розв’язок задачі

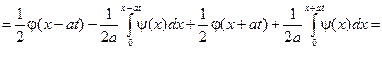
Таким чином, для задачі про поперечні коливання нескінченної струни розв’язок за методом Д’Аламбера має вигляд:

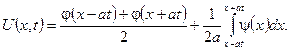(4.3)

Формула (4.3) називається розв’язком Д’Алембера задачі Коші для рівняння коливань струни.

Приклад 4.1 Знайти розв’язок задачі математичної фізики у такій постановці:

,

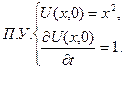
За умовою задачі функції 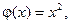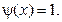За методом Д’Аламбера маємо:

Відповідь:

Дата добавления: 2014-01-04