Циклічні коди

Циклічним кодом називається лінійний блоковий (n, m) - код, в якого безліч кодових слів представляється сукупністю багаточленів ступеня (n – 1) і менш, що діляться на деякий багаточлен Р (x) ступеня k = n – m, що є співмножником двочлена (xⁿ +1). Багаточлен Р (x) називається таким, що породжує чи породжуючим. Як випливає з визначення загальна властивість кодових слів циклічного коду – це їх подільність без залишку на деякий багаточлен Р (x), званий породжуючим.

З відомих завадостійких кодів циклічні коди відрізняються високою ефективністю виявлення спотворень і порівняльною простотою реалізації кодуючих і декодуючих пристроїв. Назва цією класу кодів відбулася від їх властивості, що полягає у тому, що якщо кодова комбінація а₀, а₁, а₂,..., а _{n -1}, а _n, належать коду А, то комбінація а _n, а₀, а₁, а₂,..., а _{n -1}, одержана циклічною перестановкою елементів, також належить коду А, тобто зсув вліво на один крок будь-якого дозволеного кодового слова дає також дозволене кодове слово, що належить цьому ж коду.

Циклічні коди достатньо часто описуються з використанням багаточленів змінної х. Для побудови таких кодів цифри двійкового коду слід розглядати як коефіцієнти багаточлена змінної х, де х – основа системи числення. У двійкових кодах х = 2. Наприклад, записане в двійковому коді повідомлення 1001101 може бути представлене багаточленом виду

1· х ⁶ + 0· х ⁵ + 0· х ⁴ + 1· х ³ + 1· х ² + 0· х ¹ + 1· х ⁰ = х ⁶ + х ³ + х ² + х ⁰.

При такому представленні кодів математичні операції з отриманими багаточленами здійснюються відповідно до законів звичної алгебри, за винятком того, що складання здійснюється по модулю 2: х_а + х_а = 0, х_а + 0 = х_а,
0 + 0 = 0.

Ідея побудови циклічних кодів базується на використанні багаточленів, що не приводяться. Багаточленом, що не приводяться, називається багаточлен, який не може бути представленим у вигляді добутку багаточленів нижчих ступенів, тобто такий багаточлен ділитися тільки на самого себе або на одиницю і не ділитися ні на який інший багаточлен (аналог простих чисел). На такий багаточлен ділитися без залишку двочлен xⁿ +1. Багаточлени, що не приводяться, в теорії циклічних кодів грають роль поліномів, що утворюють, чи утворюючих поліномів.

У найбільш розповсюдженому варіанті контрольна ознака циклічного коду розраховується із застосуванням виразу, що генерує коди:

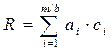(mod Р),

де як символ коду а_і розглядається вихідна т – значна інформаційна послідовність G (x), яка підлягає кодуванню. Отже, в цьому випадку, оскільки 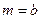та 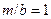, кількість доданків в сумі дорівнює одиниці (і =1). Тоді як множник слід використати величину, яка забезпечить в подальшому, після кодування, вільне місце для запису k надлишкових символів. Оскільки для цього слід забезпечити зсув інформаційної послідовність G (x), яка підлягає кодуванню, на ці ж k позицій, то ваговий коефіцієнт с_і = с повинен мати вигляд чи з використанням поліноміального запису . У результаті множення G (x) на x^k ступінь кожного одночлену, що входить в G (x), підвищується на k. Тоді вираз для розрахунку контрольної ознаки набуває вигляду:

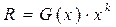(mod Р).

Як значення обраного модуля – Р використовується один із уже згаданих утворюючих поліномів P (x), ступінь якого дорівнює k. Ці поліноми вибираються із відповідних таблиць.

Операція обчислення лишку по деякому модулю, наразі це утворюючий поліном – P (x), виконується за правилом:

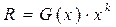(mod Р) = – [] · P (x),

де позначка [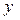] означає обчислення цілої частини від виразу в дужках. Позначимо цю цілу частину через C (x). Тоді:

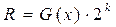(mod Р) =– C (x)· P (x), (1)

чи

F (x) = C (x) · P (x) =+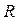. (2)

Звернемо увагу на те, що оскільки ступінь утворюючого поліному P (x) дорівнює k, частка C (x) має таку ж ступінь, як і кодова комбінація G (x), тому C (x) є кодовою комбінацією цього ж простого k -значного коду. Слід зауважити, що ступінь залишку не може бути більше ступеня утворюючого поліному, тобто його найвища ступінь дорівнює (k – 1). Отже, найбільше число розрядів залишку R (x) не перевищує числа k.

Звернемо увагу на два висновки, які витікають із аналізу виразу (2).

По-перше, після розподілу (2) на утворюючий поліном P (x) одержимо:

F (x)/ P (x) = C (x) = (x^k · G (x) + R (x))/ P (x).

Тобто сума результату множення кодової комбінації G (x) простого коду на одночлен x^k і залишку R (x)

x^kG (x) + R (x) (3)

ділиться націло на утворюючий поліном P (x):

C (x) = (x^kG (x) + R (x))/ P (x),

а отже є шуканим циклічним кодом.

По-друге, результат множення кодової комбінації С (x) простого коду на утворюючий поліном P (x):

F (x) = C (x) · P (x)

дорівнює величині (3), також ділиться націло на утворюючий поліном P (x):

F (x)/ P (x) = C (x),

а отже також є шуканим циклічним кодом.

Таким чином, процедура кодування, тобто одержання кодової комбінації циклічного n -значного коду може бути здійснена двома способами:

1) множенням кодової комбінації G (x) простого коду на одночлен x^k і додаванням до цього добутку залишку R (x), отриманого в результаті розподілу добутку x^kG (x) на утворюючий поліном P (x). Звернемо увагу, що процедура одержання залишку R (x) може бути реалізованою як R (x) = x^kG (x) mod P (x).

2) множенням інформаційної послідовності – кодової комбінації G (x) простого m - значного коду на утворюючий поліном P (x). Звернемо увагу, що остання процедура може бути реалізованою як 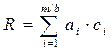(mod Р), де як символ коду а_і розглядається вихідна т – значна інформаційна послідовність G (x), яка підлягає кодуванню. Отже, в цьому випадку, оскільки 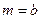та 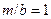, кількість доданків в сумі дорівнює одиниці (і =1). Як множник слід використати утворюючий поліном P (x), а як значення модуля – величину 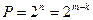, що є еквівалентним виконанню лише операції множення G (x)· P (x).

При побудові циклічних кодів першим способом розташування інформаційних символів у всіх комбінаціях строго впорядковане – вони займають m старших розрядів комбінації, а решта (k = n – m) розрядів відводяться під контрольні. Тобто, при такому методі побудови коефіцієнти при вищих ступенях х є значеннями інформаційних розрядів, а коефіцієнти при ступенях порядку (k – 1) і нижче - є перевірочними. Нагадаємо, що такі коди мають назву роздільних несистематичних (надлишкові символи мають чітко визначені позиції і не є лінійними комбінаціями інформаційних).

При другому способі утворення циклічних кодів інформаційні і контрольні символи в комбінаціях циклічного коду не відокремлені один від одного, що утрудняє процес декодування. Такі коди мають назву нероздільних систематичних (надлишкові символи не мають чітко визначених позицій і є лінійними комбінаціями інформаційних).

Приклад реалізації першого способу кодування. Дано: n = 7, m = 4,
k = 3 і Р (x) = х³ + х + 1 = 1011. Потрібно закодувати повідомлення
G (x) = х ³ + х ²+ + 1 = 1101.

Множимо кодову комбінацію G (x) вихідного коду на одночлен x^k = х ³, і одержуємо x^k·G (x) = х⁶ + х⁵ + х³. Надалі ділимо цей добуток на утворюючий поліном Р (x) = х³ + х + 1, в наслідок чого одержимо:

х⁶ + х⁵ + х³ х³ + х + 1

х⁶ + х⁴ + х³ х³ + х² + х+ 1

х⁵ + х⁴

х⁵ + х³ + х²

х⁴+ х³ + х²

х⁴+ х² + х

х³ + х

х³ + х + 1

R (x) = 1

У результаті цій операції одержимо залишок R (x) = 1.

Додаючи добуток х ³ G (х) до одержаного залишку, одержимо кодовий багаточлен

F (x) = x ³ G (х) + R (x) = х ⁶ + х ⁵ + х ³+ 1.

У двійковому коді цьому багаточлену відповідає кодова комбінація 1101001, в якій перевірочні розряди займають три останні позиції і яку слід передавати каналом зв’язку.

В разі відсутності спотворень на приймальному боці прийнята кодова комбінація F^/ (x) повністю збігається із переданою F^/ (x) = F (x) = х ⁶ + х ⁵ + х ³+ 1 і повинна ділитися на утворюючий багаточлен Р (x) без залишку:

У результаті цій операції одержимо частку С (x) = х³ + х² + х + 1 та залишок R (x) = 0, що відповідає нашім очікуванням.

х ⁶ + х ⁵ + х ³ + 1 х³ + х + 1

х⁶ + х⁴ + х³ х³ + х² + х + 1

х⁵ + х⁴ + 1

х⁵ + х³ + х²

х⁴ + х³ + х² + 1

х⁴ + х² + х

х³ + х + 1

х³ + х + 1

R (x) = 0

Приклад реалізації другого способу кодування. Дано: n = 7, m = 4, k = = 3 і Р (x) = х³ + х + 1= 1011. Потрібно закодувати повідомлення х ³ + х ² + х ⁰ =
= 1101.

Для кодування даного повідомлення 1101, відповідного багаточлену
G (х) = х ³ + х ² + 1, помножимо Р (х) на G (х):

х³ + х + 1

х³ + х² + 1

х³ + х + 1

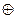х⁵ + х³ + х²

х⁶ + х⁴+ х³

х⁶ + х⁵ + х⁴ + х³ + х² + х + 1

У двійковому коді цьому багаточлену відповідає кодова комбінація

F (x) = G (х) · Р (x) = х⁶ + х⁵ + х⁴ + х³ + х² + х + 1 = 1111111,

яку слід передавати каналом зв’язку і в якій контрольні символи не відокремлені один від одного. Отже маємо нероздільний систематичний код (надлишкові символи не мають чітко визначених позицій і є лінійними комбінаціями інформаційних).

В разі відсутності спотворень ця кодова комбінація повинна ділитися на утворюючий багаточлен Р (x) без залишку:

х⁶ + х⁵ + х⁴ + х³ + х²+ х + 1 х³ + х + 1

х⁶ + х⁴ + х³ х³ + х² + 1

х⁵ + х² + х + 1

х⁵ + х³ + х²

х³ + х + 1

х³ + х + 1

R (x) = 0

У результаті цій операції одержимо частку С (x) = х³ + х² + 1 та залишок R (x) = 0, що відповідає нашім очікуванням. Звернемо увагу, що частка С (x) є тим повідомленням, яке кодувалося циклічним кодом.

Розглянуті міркування надають можливість стверджувати наступне. В разі наявності спотворень прийняте повідомлення, яке позначимо F ^/(x), можна представити у вигляді суми двох доданків: багаточлена, сформованого на передаючій стороні F (x), і багаточлена спотворення Е (х): F ^/(x) = F (x) + Е (х). Цей багаточлен слід розділити на Р (х).

F ^/(x) = (F (x) + Е (х))/ Р (х) = F (x) / Р (х) + Е (х)/ Р (х).

Якщо ділення здійснюється без залишку, що є можливим лише при
Е (х) = 0, оскільки F (x) / Р (х) = 0 за визначенням коду, то ухвалюється рішення, що інформація не спотворена. В іншому випадку слід ухвалити рішення, що інформація має спотворення.

Отже, процедура декодування, при застосуванні циклічного коду в режимі виявлення спотворень, полягає, перш за все, у визначенні факту відсутності чи наявності спотворень. Із цією метою, незалежно від процедури кодування, здійснюється розподіл прийнятого повідомлення F ^/(x) на утворюючий поліном Р (х) та аналіз одержаного при цьому залишку.

Якщо ділення здійснюється без залишку, то ухвалюється рішення, що інформація не спотворена. Тоді, в разі використання першого способу кодування, прийнятим вважається повідомлення, одержане шляхом відкидання від прийнятого поліному F ^/(x) усіх членів, ступінь яких є меншою за k. У разі ж використання другого способу кодування, прийнятим вважається повідомлення, яке є часткою від розподілу прийнятого повідомлення F ^/(x) на утворюючий поліном Р (х), тобто поліном С (x).

Якщо ділення здійснюється із залишком, то прийнята інформація має спотворення, не може бути використаною для подальших операцій над нею і ухвалюється рішення, щодо подальших кроків.

У разі застосування циклічного коду, як коду з виправленням спотворень, процедура декодування включає аналіз залишку, що одержано після ділення прийнятої кодової комбінація на утворюючий багаточлен, визначення місця спотворення та його усунення. Ця процедура розглядається нижче.

Одна з основних задач, що стоять перед розробниками захисних пристроїв від помилок при передачі дискретних повідомлень по каналах зв’язку є вибір породжуючого багаточлена Р (x) для побудови циклічного коду, що забезпечує необхідну мінімальну кодову відстань для гарантійного виявлення та виправлення t-кратних спотворень.

Існують спеціальні таблиці з вибору Р (x) в залежності від пропонованих вимог до корегуючих можливостям коду. Приклад такої таблиці (табл. 1) наведено. Однак у кожного циклічного коду є свої особливості формування Р (x). Тому при вивченні конкретних циклічних кодів розглядаються відповідні способи побудови Р (x).

Таблица 1

k -ступінь поліному G (х)	Породжуючий поліном G (х)	Запис поліному по mod 2	Запис поліному по mod 8	n	m	Примітка
	x +1	11	3	3	2	Код с перевіркою на парність
	x ^2+ x +1	111	7	3	1	Код с повторенням
	x ^3+ x ^2+1	1101	13	7	4	Класичний код
x ^3+ x +1	1011	15	7	4	Код Хеммінга
	x ^4+ x ^3+1	11001	31	15	11	Класичний код
x ^4+ x +1	10011	23	15	11	Код Хеммінга
x ^4+ x ^2+ x +1	10111	27	7	3	Коди Файра- Абрамсона
x ^4+ x ^3+ x ^2+1	11101	35	7	3
	x ^5+ x ^2+1	100101	45	31	26	Класичний код
x ^5+ x ^3+1	101001	51	31	26	Код Хеммінга
…	…	…	…	…
	x ^6+ x ^5+ x ^4+ + x ^3+ x ^2+ x ^1+1	1111111	177	7	1	Код с повторенням
	...	...	...

Дата добавления: 2014-01-04