Властивості циклічних кодів

Серед основних властивостей циклічного коду можна визначити:

1) Якщо прийнята комбінація ділиться на багаточлен, який утворює, без залишку, то код прийнятий безпомилково.

Приклад 1. Нехай, як в прикладі, наведеному вище, при повідомленні 1011, m = 4, коли утворюючий багаточлен Р (x) = х ³ + х ² + х ⁰, одержана кодова комбінація F (x) = 1011100, в якій перевірочні розряди займають три останні позиції.

Нехай прийнята комбінація не має спотворень: . Розділемо прийняту комбінацію F (x) на багаточлен, який утворює:

х ⁶ + х ⁴ + х ³ + х ² х ³ + х ² + 1

х ⁶ + х ⁵ + х ³ х ³ + х ²

х ⁵ + х ⁴+ х ²

х ⁵ + х ⁴ + х ²

= 0

Оскільки залишок дорівнює нулю, то спотворень не виявлено.

2) Циклічний код виявляє всі одиночні помилки, якщо утворюючий поліном містить більш за одного члена. Якщо G (x) = x + 1, то код виявляє одиночні помилки і всі непарні;

3) Циклічний код з G (x) = (x+ 1) G (x) виявляє всі одиночні, подвійні і потрійні помилки;

4) Циклічний код із утворюючим поліномом G (x) ступеня k = n - m виявляє всі групові помилки тривалістю в k символів.

5) Циклічний зсув не спотвореної (дозволеної) комбінації циклічного коду дає дозволену комбінацію. Отже, зсув не спотвореної (дозволеної) комбінації циклічного коду на будь-яку кількість розрядів не виявляється (дає дозволену комбінацію).

Дійсно, такий зсув, наприклад на і розрядів, є еквівалентним множенню вихідної комбінації на величину x^і, тобто перетворенню типу F (x) → x^і· F (x). Тоді при перевірці на наявність спотворень результат ділення зсунутої комбінації на утворюючий поліном: x^і·F (x)/ Р (x) = x^і· [ F (x)/ Р (x)] = x^і· 0 = 0 дає в наслідку залишок, який дорівнює нулю, що призводить до висновку щодо відсутності спотворень (наявності дозволеної комбінації).

Приклад 2. Циклічний зсув одержаної в прикладі 1 комбінації має вигляд F_ц (x) = 0111001 = х ⁵ + х ⁴ + х ³ + 1 і повинен дати дозволену комбінацію. Для перевірки цього розділімо одержану комбінацію F_ц (x) на утворюючий поліном:

х ⁵ + х ⁴ + х ³+ 1 х ³ + х ² + 1

х ⁵ + х ⁴ + х ² х ² + 1

х ³ + х ²+ 1

х ³ + х ² +1

R (x) = 0

Наявність залишку, який дорівнює нулю, свідчить про правильність цього твердження.

6) Наявність відмінного від нуля залишку від ділення F (x)/ Р (x) свідчить про наявність спотворення, але не вказує, якого саме.Дійсно наявність спотворення є еквівалентним тому, що передана комбінація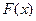 перетворилася в комбінацію: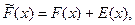де: 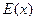– вектор спотворень. Результат ділення прийнятої комбінації 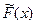на багаточлен, який утворює 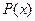, слід розглядати як такий, що складається із двох доданків: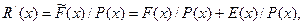де перший доданок, виходячи із властивостей коду, дорівнює нулю, .

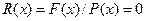Звернемо увагу на те, що одержаний результат ділення встановлює однозначну відповідність між та 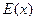і є ознакою наявності (синдромом) спотворення відповідного символу.

Ця властивість надає принципову можливість визначення, при певних умовах, і місця спотворення.

Дата добавления: 2014-01-04