Числовые характеристики двумерных случайных величин

Некоторые числовые характеристики одномерных случайных величин: начальные и центральные моменты, мода, медиана, квантиль, коэффициенты асимметрии и эксцесса. Числовые характеристики двумерных случайных величин: начальные и центральные моменты. Корреляционный момент и коэффициент корреляции. Коррелированность и зависимость случайных величин.

Лекция 9.

Двумерные случайные величины.

Случайные векторы (системы нескольких случайных величин). Закон распределения веро-ятностей дискретной двумерной случайной величины. Функция распределения и плот-ность распределения двумерной случайной величины, их свойства. Вероятность попада-ния случайной точки в произвольную область. Отыскание плотностей вероятности со-ставляющих двумерной случайной величины. Равномерное распределение на плоскости.

Лекция 8.

Наряду с одномерными случайными величинами, возможные значения которых определяют-ся одним числом, теория вероятностей рассматривает и многомерные случайные величины. Каждое возможное значение такой величины представляет собой упорядоченный набор нескольких чисел. Геометрической иллюстрацией этого понятия служат точки п -мерного пространства, каждая координата которых является случайной величиной (дискретной или непрерывной), или п -мерные векторы. Поэтому многомерные случайные величины называют еще случайными векторами.

1. Дискретные двумерные случайные величины.

Закон распределения дискретной двумерной случайной величины (Х, Y) имеет вид таблицы с двойным входом, задающей перечень возможных значений каждой компоненты и вероятности p (x_i, y_j), с которыми величина принимает значение (x_i, y_j):

Y	Х
x 1	x 2	…	xi	…	xn
y 1	p (x 1, y 1)	p (x 2, y 1)	…	p (xi, y 1)	…	p (xn, y 1)
…	…	…	…	…	…	…
yj	p (x 1, yj)	p (x 2, yj)	…	p (xi, yj)	…	p (xn, yj)
…	…	…	…	…	…	…
ym	p (x 1, ym)	p (x 2, ym)	…	p (xi, ym)	…	p (xn, ym)

При этом сумма вероятностей, стоящих во всех клетках таблицы, равна 1.

Зная закон распределения двумерной случайной величины, можно найти законы распреде-ления ее составляющих. Действительно, событие Х = х ₁ представляется собой сумму несовместных событий (X = x ₁, Y = y ₁), (X = x ₁, Y = y ₂),…, (X = x ₁, Y = y_m), поэтому

р (Х = х ₁) = p (x ₁, y ₁) + p (x ₁, y ₂) +…+ p (x ₁, y_m) (в правой части находится сумма вероятностей, стоящих в столбце, соответствующем Х = х ₁). Так же можно найти вероятности остальных возможных значений Х. Для определения вероятностей возможных значений Y нужно сложить вероятности, стоящие в строке таблицы, соответствующей Y = y_j.

Пример 1. Дан закон распределения двумерной случайной величины:

Y	X
-2
-0,8	0,1	0,3	0,1
-0,5	0,15	0,25	0,1

Найти законы распределения составляющих.

Решение. Складывая стоящие в таблице вероятности «по столбцам», получим ряд распре-деления для Х:

Х	-2
р	0,25	0,55	0,2

Складывая те же вероятности «по строкам», найдем ряд распределения для Y:

Y	-0,8	-0,5
p	0,5	0,5

Определение 9.1. Начальным моментом порядка k случайной величины Х называется матема-тическое ожидание величины X^k:

ν _k = M (X^k). (9.1)

В частности, ν₁ = М (Х), ν₂ = М (Х ²). Следовательно, дисперсия D (X) = ν₂ – ν₁².

Определение 9.2. Центральным моментом порядка k случайной величины Х называется мате-матическое ожидание величины (Х – М (Х)) ^k:

μ _k = M ((Х – М (Х)) ^k). (9.2)

В частности, μ₁ = M (Х – М (Х)) = 0, μ₂ = M ((Х – М (Х))²) = D (X).

Можно получить соотношения, связывающие начальные и центральные моменты:

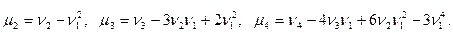
Мода и медиана.

Такая характеристика случайной величины, как математическое ожидание, называется иногда характеристикой положения, так как она дает представление о положении случайной величии-ны на числовой оси. Другими характеристиками положения являются мода и медиана.

Определение 9.3. Модой М дискретной случайной величины называется ее наиболее вероятное значение, модой М непрерывной случайной величины – значение, в котором плотность вероятности максимальна.

Пример 1.

Если ряд распределения дискретной случайной величины Х имеет вид:

Х
р	0,1	0,7	0,15	0,05

то М = 2.

Пример 2.

Для непрерывной случайной величины, заданной плотностью распределения , модой является абсцисса точки максимума: М = 0.

Замечание 1. Если кривая распределения имеет больше одного максимума, распределение называется полимодальным, если эта кривая не имеет максимума, но имеет минимум – анти-модальным.

Замечание 2. В общем случае мода и математическое ожидание не совпадают. Но, если распре-деление является симметричным и модальным (то есть кривая распределения симметрична от-носительно прямой х = М) и имеет математическое ожидание, оно совпадает с модой.

Определение 9.4. Медианой Ме непрерывной случайной величины называют такое ее значение, для которого

p (X < Me) = p (X > Me). (9.3)

Графически прямая х = Ме делит площадь фигуры, ограниченной кривой распределения, на две равные части.

Замечание. Для симметричного модального распределения медиана совпадает с математичес-ким ожиданием и модой.

Определение 9.5. Для случайной величины Х с функцией распределения F (X) квантилью порядка р (0 < p < 1) называется число К_р такое, что F (K_p) ≤ p, F (K_p + 0) ≥ p. В частности, если F (X) строго монотонна, К_р: F (K_p) = p.

Такие характеристики, как начальные и центральные моменты, можно ввести и для системы двух случайных величин.

Определение 9.8. Начальным моментом порядка k, s двумерной случайной величины (Х, Y) называется математическое ожидание произведения X^k на Y^s:

α _k,s = M (X^kY^s). (9.6)

Для дискретных случайных величин 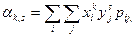для непрерывных случайных величин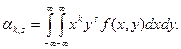

Определение 9.9. Центральным моментом порядка k, s двумерной случайной величины (Х, Y) называется математическое ожидание произведения (X – M (X)) ^k на (Y – M (Y)) ^s:

μ _k,s = M ((X – M (X)) ^k (Y – M (Y)) ^s). (9.7)

Для дискретных случайных величин для непрерывных случайных величин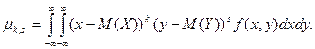

При этом М (Х) = α_1,0, M (Y) = α_0,1, D (X) = μ_2,0, D (Y) = μ_0,2.

Дата добавления: 2014-01-04