Формула Аккермана

Если исходное уравнение состояния объекта отличается от управляемой канонической формы, то в случае управляемости объекта для определения вектора обратной связи по состоянию используют следующую трехэтапную процедуру.

1. Преобразуют исходную модель объекта в управляемую каноническую форму, используя матрицу преобразования

. (*)

2. Находят вектор обратной связи по преобразованному состоянию , применяя (18).

3. Преобразуют вектор в вектор обратной связи по исходному состоянию 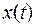. используя

. (19)

Формула Аккермана объединяет эти шаги в одну формулу

, (20)

где матричный многочлен 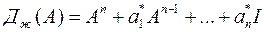составлен с помощью коэффициентов характеристического уравнения желаемой системы.

Пример. Пусть объект описывается уравнением состояния

,

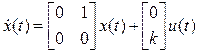а желаемый характеристический многочлен имеет вид .

Так как

,

то передаточная функция объекта имеет вид , т.е. объект представляет собой двойной интегратор. Отсюда, . Следовательно, n= 2, и матрица управляемости

.

В соответствии с (**) обратная матрица

.

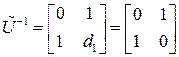Легко показать, что

, ,

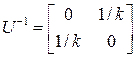так что согласно (*)

.

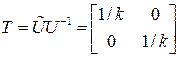Используя (18) , ,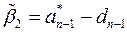…,,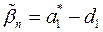 находим

, .

Согласно (19)

,

что совпадает с выражением, полученным ранее другим путем.

Команда MATLAB: acker (A,B, Р_р).

Пример. Пусть в условиях предыдущего примера коэффициенты 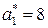, , так что полюсы желаемой системы , k = 1. Тогда применяя команду

l = acker(A,B, [-4+j*4 -4-j*4]),

можно найти .

Сделаем несколько замечаний, касающихся рассмотренного метода размещения полюсов.

1. Матрица T может быть найдена только в том случае, когда существует обратная матрица управляемости 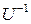. Следовательно, любое расположение полюсов проектируемой системы с помощью обратной связи по состоянию можно обеспечить, если объект управления полностью управляем, т.е. если матрица управляемости объекта 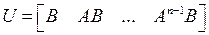является невырожденной, так что .

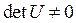2. Спроектированная в соответствии с формулами (7), (18) и (19) система не удовлетворяет условию астатизма, т.е. ее передаточная функция

не равна единице при p =0, другими словами, спроектированная система является статической. Здесь K (p) числитель ПФ объекта.

Если выбрать закон управления в виде

,

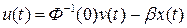то передаточная функция проектируемой системы

.

Так как 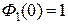, то, как видим, введение наряду с обратной связью по состоянию прямой связи по задающему воздействию

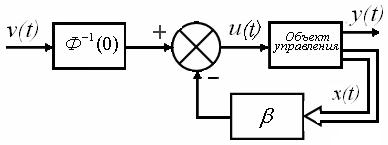
Рис.3

(рис. 3) обеспечивает астатизм проектируемой системы.

Дата добавления: 2014-01-04