Определение и свойства многочленов Чебышева

ИНТЕРПОЛИРОВАНИЕ И АППРОКСИМАЦИЯ

Определение 18.1. Многочленом Чебышева называется функция

Т_n (х):= cos(n arccos х), (18.1)

где n Î N₀, x Î [-1,1].

Прежде всего убедимся, что функция Т_n (х), представленная с помощью тригонометрических функций, на самом деле является многочленом при любом n Î N₀.

Непосредственной подстановкой в (18.1) значений п = 0 и п = 1 получаем Т ₀ (х) = 1, Т ₁ (х) = х.

Положив а:= arccos x, имеем:

Т ₁ (х) = cos а, Т_n (х) = cos па, Т_{n -1} (х) = cos(n - 1) а, Т_{п+ 1} (х) = соs(n + 1) а,

и так как (по формуле суммы косинусов)

соs(n + 1) а + cos(n - 1) а = 2 cos a cos па,

то, значит, справедливо равенство

Т_{п+ 1} (х) + Т_{n -1} (х) = 2 Т_n (х) Т ₁ (х),

которое может быть переписано в виде

Т_{п+ 1} (х) + Т_{n -1} (х) = 2 Т_n (х) Т ₁ (х). (18.2)

Формула (18.2) определяет при п = 1, 2, 3 ,... последовательность функций Т_п (х), начинающуюся с Т ₀ (х) = 1, Т ₁ (х) = х, рекуррентно; при этом нужно иметь в виду, что здесь x Î [-1,1], как и в (18.1).

Подставляя в (18.2) заданные начальные члены последовательности { Т_n (х)}, найдем несколько ее последующих членов:

Т ₂(х) = 2 х ² - 1;

Т ₃ (х) = 4 х ³ - 3 х;

Т ₄ (х) = 8 х ⁴ - 8 х ² +1;

и т.д.

Графики нескольких многочленов Чебышева (с первого по четвертый) изображены на рис.18.1.

Рис. 18.1.

Анализ рекуррентной формулы (18.2) позволяет считать очевидными следующие факты:

1) все функции Т_n (х), определенные в (18.1), являются многочленами при любом натуральном п;

2) степени этих многочленов возрастают с увеличением п, причем старший член многочлена Т_n (х) равен 2 ^{n- 1} хⁿ;

3) многочлены Т_n (х) при четных п выражаются через степенные функции только четных степеней, при нечетных — только нечетных.

Наряду с многочленами Чебышева Т_n (х) часто используют многочлены, получаемые из Т_n (х) делением на старший коэффициент, т.е.

— многочлены со старшим коэффициентом 1. Будем называть их нормированными многочленами Чебышева.

Многочлены Чебышева обладают рядом замечательных свойств. Рассмотрим некоторые их свойства,имеющие отношение к поставленной выше проблеме аппроксимации функций.

Свойство 18.1. Многочлен Чебышева Т_n (х) имеет на отрезке [-1,1] ровно п различных действительных корней; все они задаются формулой

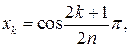, где k = 0,1,..., п- 1.

Свойство 18.2. Корни многочленов Чебышева перемежаются с точками их наибольших и наименьших значений, равных соответственно + 1 и -1 для Т_n (х), а именно функция Т_n (х), имеет экстремумы Т_n (х_j)= (- 1) ^j в точках

Свойство 18.3 (теорема Чебышева). Из всех многочленов степени п со старшим коэффициентом 1 нормированный многочлен Чебышева Т_n (х) наименее уклоняется от нуля на отрезке [ - 1,1].

Дата добавления: 2014-01-04