Системы линейных однородных уравнений. Фундаментальная система решений

Система линейных уравнений с 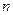переменными называется системой линейных однородных уравнений, если все их свободные члены равны нулю. Такая система имеет вид:

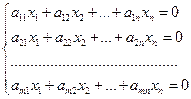(10)

Система линейных однородных уравнений всегда совместна, так как она всегда имеет, по крайней мере, нулевое (или тривиальное) решение .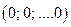

Если в системе (10) 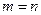, а ее определитель отличен от нуля, то такая система имеет только нулевое решение, как это следует из теоремы Крамера. Ненулевые решения, следовательно, возможны лишь для таких систем линейных однородных уравнений, в которых число уравнений меньше числа переменных или при их равенстве, когда определитель системы равен нулю.

Иначе: система линейных однородных уравнений имеет ненулевые решения тогда и только тогда, когда ранг ее матрицы коэффициентов при переменных меньше числа переменных, т.е. при .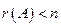

Обозначим решение системы (10) 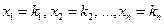в виде строки .

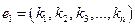Решения системы линейных однородных уравнений обладают следующими свойствами:

1. Если строка 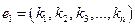- решение системы (10), то строка 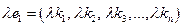- также решение этой системы.

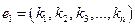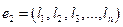2. Если строки и - решения системы (10), то при любых 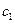и 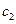их линейная комбинация 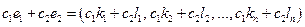- также решение данной системы.

Из сформулированных свойств следует, что всякая линейная комбинация решений системы линейных однородных уравнений также является решением этой системы.

Определение. Система линейно независимых решений 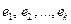называется фундаментальной, если каждое решение системы (10) является линейной комбинацией решений .

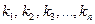Теорема. Если ранг 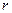матрицы коэффициентов при переменных системы линейных однородных уравнений (10) меньше числа переменных 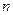, то всякая фундаментальная система решений (10) состоит из 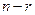решений.

Поэтому общее решение системы (10) линейных однородных уравнений имеет вид

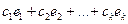
где 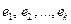- любая фундаментальная система решений; 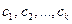- произвольные числа;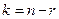

Для нахождения фундаментальной системы решений системы уравнений (10) ее 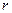основных (базисных) переменных (с отличным от нуля базисным минором) выражают через неосновные (свободные) переменные. Затем поочередно заменяют 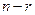неосновных переменных элементами каждой строки невырожденной квадратной матрицы порядка 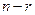, например, единичной .

Пример 3. Для системы уравнений, приведенной в примере 1, найти фундаментальную систему решений соответствующей однородной системы уравнений.

Решение. Выразим основные переменные через неосновные :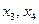

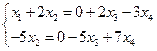
(в отличие от примера 1 здесь свободные члены уравнений равны нулю).

Для нахождения фундаментальной системы решений заменяем поочередно неосновные переменные 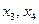элементами строк единичной матрицы .

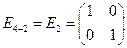При 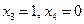получим из второго уравнения и из первого 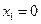, т.е. .

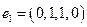При 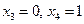получим из второго уравнения 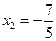и из первого 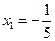, т.е. .

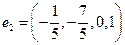Итак, фундаментальную систему решений образуют строки 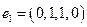и .

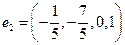Теорема. Общее решение системы (1) линейных уравнений с 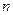переменными равно сумме общего решения соответствующей ей системы однородных линейных уравнений (10) и произвольного частного решения системы (1)

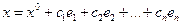
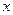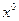где и - соответственно общее и частное решение системы (1); 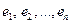- фундаментальная система решений системы (10)

Пример 4. По данным примера 1 убедиться в справедливости теоремы об общем решении системы линейных уравнений.

Решение. В примере 1 было получено общее решение системы виде , где 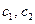- любые числа.

Найдем произвольное частное решение системы, например, базисное решение при 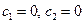, т.е. .

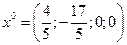В примере 3 была получена фундаментальная система решении 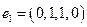, 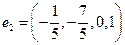соответствующей однородной системы уравнений.

Итак,

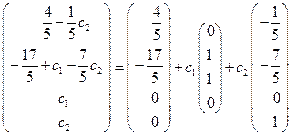
где 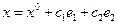, где первый столбец в правой части равенства – частное решение 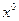неоднородной системы уравнений, а два последних – фундаментальная система решений соответствующей однородной системы.

Дата добавления: 2014-01-05