Собственные значения и собственные векторы матрицы

Опред. Число называется собственным значением матрицыпорядка 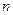, если существует такой ненулевой вектор , что выполняется равенство

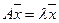(44)

При этом 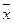называется собственным вектором матрицы.

Множество всех собственных значений матрицы называется ее спектром.

Собственные значения и собственные векторы линейного оператора Опред. Вектор 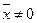называется собственным вектором линейного оператора 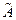(или матрицы ), если найдется такое число , что (47)исло называется собственным значением (числом) оператора 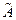(или матрицы ), соответствующий ветру 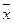(Собственные векторы и собственные значения в литературе называют также характеристическими векторами и значениями

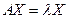
Свойства собственных значений матрицы

линейного оператора .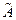

1. Произведение собственных значений матрицы равно ее определителю

.

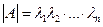2. Число отличных от нуля собственных значений матрицы равно ее рангу.

3. Все собственные значения матрицы отличны от нуля тогда и только тогда, когда матрица невырожденная.

4. Если 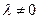- собственное значение невырожденной матрицы , то 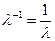- собственное значение обратной матрицы .

5. Если l - собственное значение матрицы , - собственное значение матрицы 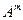, где 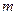- натуральное число.

Диагональная форма матрицы оператораматрица является диагональной:

.

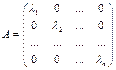Следовательно, для того чтобы привести матрицу оператора 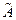к диагональному виду согласно формуле 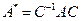, в качестве матрицы нужно взять матрицу, столбцами которой должны быть собственные векторы оператора .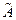

Квадратичные формы.

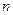Опред. Квадратичной формой от переменных называется сумма, каждый член которой является либо квадратом одной из переменных, либо произведением двух разных переменных, взятых с некоторым коэффициентом:

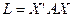
Преобразование квадратичных форм.

Итак, при невырожденном линейном преобразовании матрица квадратичной формы принимает вид

Канонический и нормальный виды квадратичной формы.

Определение. Квадратичная форма называется канонической или имеет канонический вид, если все ее коэффициенты 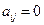при :

т.е. матрица является диагональной.

Теорема. Любая кВ. форма с помощью невырожденного лин. Преобраз. Перемен. может быть приведена к каноническому виду.

Опред. Кв. форма с действительными коэффициентами имеет нормальный вид, если в ее каноническом виде все коэффициенты равны 1 или -1.

Метод Лагранжа. Заключается в выделении полных квадратов: сначала формируется полный квадрат из слагаемых, содержащих , затем из слагаемых, содержащих и т.д. Рассмотрим это на конкретном примере.

Критерий знакоопределенности квадратичной формы.

Опред. Кв. форма (50) называется положительно определенной (отрицательно определенной), если для любых значений перемен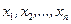, не равных одновременно нулю, указанная форма имеет положит (отрицательные) значения.

Оба этих случая объединены под названием знакоопределенных форм. Если кВ. форма (как полож, так и отриц знач, то она назя знакопеременной.

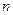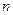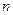Кв. форма отпеременных является положит определенной, тогда и только тогда, если ее норм вид содержит ровно квадратов, т.е. имеет вид . Понятно, что все собственных значений матрицы квадратичной формы должны быть положительными.

Аналогично в нормальный вид отрицательно определенной все 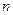квадратов должны входить со знаком минус, т.е. все 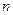собственных значений матрицы квадратичной формы должны быть отрицательными.

Теорема. (критерий Сильвестра). Для того чтобы квадратичная форма была положительно определенной, необходимо и достаточно, чтобы были выполнены условия

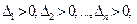
Для того, чтобы квадратичная форма была отрицательно определенной, необходимо и достаточно, чтобы знаки главных миноров чередовались, причем .

Дата добавления: 2014-01-05