Свойства взаимно простых чисел

1. 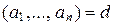Û .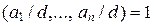

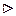Необходимость. Согласно следствию из теоремы 1.2.3 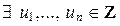, такие, что 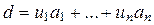, следовательно, 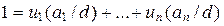, зна-чит, 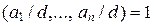по теореме 1.4.1.

Достаточность. 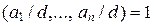, следовательно, 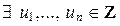, такие, что 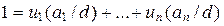(согласно теореме 1.4.1), откуда d = u ₁ a ₁ +…+ + u_na_n. Значит, по свойству 5 делимости целых чисел, а поскольку , то по определению НОД, следовательно, .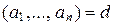

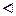
2. с | ab & (c, a) = 1 Þ с | b.

При b ¹ 0 $ t, u, v Î Z, такие, что ab = ct & cu + av = 1 Þ cub + ctv = b Þ Þ с | b по свойству 5 делимости целых чисел. При b = 0 доказательство очевидно согласно свойству 1 делимости целых чисел.

3. & .

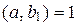Необходимость.

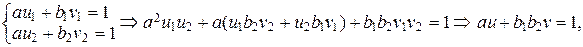
где 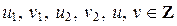. Значит, согласно теореме 1.4.1.

Достаточность. Пусть 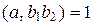. Если предположить, что 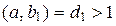или , то согласно свойству 3 делимости целых чисел и определению НОД получим, чт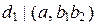о либо . Это противоречит тому, что 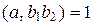. Значит, & .

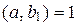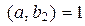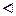
4. Следствие из свойства 3. Простое число p делит произведение , k Î N, тогда и только тогда, когда 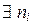, 1 £ i £ k, со свойством .

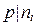Необходимость. Если с указанным свойством, то по свойству 1 простых чисел , значит, по свойству 3 взаимно простых чисел, следовательно, 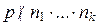снова по свойству 1 простых чисел, что приводит к противоречию. Итак, 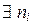, 1 £ i £ k, со свойством .

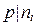Достаточность. Если 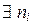, 1 £ i £ k, со свойством 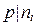, то по свойству 3 делимости целых чисел.

С помощью свойств взаимно простых чисел и метода математической индукции доказывается следующая важная теорема.

Теорема 1.4.2 (основная теорема арифметики). Всякое натуральное число n > 1 однозначно раскладывается в произведение простых чисел с точностью до порядка следования множителей:

, . (1.4.1)

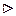n = 2 – база индукции. Предположим, что утверждение верно для .

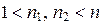Для простого числа n доказательство очевидно, s = 1. Пусть – составное число, . Воспользуемся предположением индукции и разложим на простые множители и 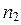, тем самым в произведение простых чисел будет разложено и n.

Пусть и 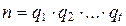, s, t Î N, – два разложения числа n на простые множители. Тогда, воспользовавшись свойством 4 взаимно простых чисел и свойством 1 простых чисел и последовательно сокращая обе части равенств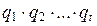а = на 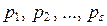, приходим к выводу, что s = t и с точностью до порядка следования множителей 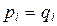, 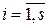. Таким образом, разложение (1.4.1) числа n однозначно с точностью до порядка следования множителей.

Определение 1.4.2. Если в равенстве (1.4.1) собрать одинаковые множители в степени, то получим каноническое разложение натурального числа n > 1: 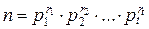, где 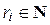, , 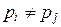при i ¹ j. Если z – целое, не равное 0, ±1 число, то – каноническое разложение .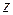

Пример 1.4.1. Найдем разложения вида (1.4.1) и канонические разложения целых чисел.

1. – 484 = – 2 × 242 = – 2 × 2 × 121 = – 2 × 2 × 11 × 11 = – 2² × 11².

2. 2¹² – 1 = 4095 = 3 × 1365 = 3 × 3 × 455 = 3 × 3 × 5 × 91 = 3 × 3 × 5 × 7 × 13 = = 3² × 5 × 7 × 13. ·

По каноническому разложению целых чисел легко находятся их НОД и НОК, решаются иные задачи.

Пусть – ненулевые целые числа, хотя бы одно из которых отлично от . Запишем их канонические разложения:

, , , , ,

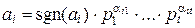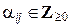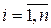где p ₁,…, p_t – простые числа, входящие во все разложения 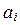, , 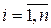причем в случае отсутствия множителя p_j в разложении 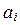полагается a _ij = 0. Тогда, исходя из определений, получаем следующие формулы для канонических разложений НОД и НОК чисел :

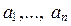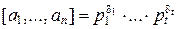, где , ,

, где , .

Дата добавления: 2014-01-05