
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Перестановки
|
|
|
|
Пусть  последовательность натуральных чисел, а
последовательность натуральных чисел, а 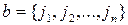 — последовательность тех же чисел, но взятых в другом (том же) порядке.
— последовательность тех же чисел, но взятых в другом (том же) порядке.
Определение 2.3.1. Последовательность b называется перестановкой последовательности a.
Лемма 2.3.1. Число различных перестановок последовательности a равно n! .
.
Доказательство. Так как среди чисел 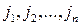 нет одинаковых, то в качестве первого числа
нет одинаковых, то в качестве первого числа  можно взять любое из чисел от 1 до n. Поэтому имеем ровно n вариантов выбора. В качестве второго числа
можно взять любое из чисел от 1 до n. Поэтому имеем ровно n вариантов выбора. В качестве второго числа  можно взять любое из n – 1 оставшихся, т. е. имеем n – 1 вариантов выбора. Таким образом, получаем n (n – 1) различных способов выбора первых двух элементов. Продолжая аналогичные рассуждения, убеждаемся, что число различных перестановок из n чисел равно n!
можно взять любое из n – 1 оставшихся, т. е. имеем n – 1 вариантов выбора. Таким образом, получаем n (n – 1) различных способов выбора первых двух элементов. Продолжая аналогичные рассуждения, убеждаемся, что число различных перестановок из n чисел равно n!
Определение 2.3.2. Будем говорить, что пара элементов  ,
, 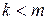 , перестановки b образуют инверсию, если
, перестановки b образуют инверсию, если  . Число всех пар перестановки b, образующих инверсию, называется числом инверсий в b и обозначается
. Число всех пар перестановки b, образующих инверсию, называется числом инверсий в b и обозначается 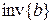 .
.
Определение 2.3.3. Перестановка, содержащая четное число инверсий, называется четной, а нечетное число — нечетной.
Определение 2.3.4. Если в некоторой перестановке j- й и k -й элементы поменять местами, оставив без изменения положение остальных  элементов, то такая операция называется транспозицией и обозначается (j, k).
элементов, то такая операция называется транспозицией и обозначается (j, k).
Теорема 2.3.1. Если в некоторой перестановке сделана транспозиция, то она равна произведению нечетного числа транспозиций соседних элементов.
Доказательство. Пусть дана некоторая перестановка  . Допустим, что в результате транспозиции (k, s) элементы
. Допустим, что в результате транспозиции (k, s) элементы 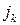 и
и 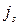 поменялись местами. Число элементов между ними равно
поменялись местами. Число элементов между ними равно 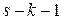 . Меняем местами
. Меняем местами  и
и 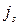 , затем
, затем  и
и 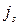 и т. д. После
и т. д. После 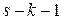 транспозиций получаем перестановку
транспозиций получаем перестановку 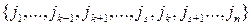 . Меняем теперь местами
. Меняем теперь местами 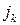 и
и 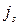 , потом
, потом 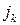 и
и  и т. д. В результате
и т. д. В результате  транспозиций приходим к исходной перестановке. Всего совершено нечетное число
транспозиций приходим к исходной перестановке. Всего совершено нечетное число  транспозиций соседних элементов.
транспозиций соседних элементов.
|
|
|
Теорема 2.3.2. При транспозиции соседних элементов число инверсий в перестановке меняется на единицу.
Доказательство. Допустим, что в перестановке  сделана транспозиция
сделана транспозиция  , получаем
, получаем  Понятно, что число инверсий в перестановках, не содержащих элементы
Понятно, что число инверсий в перестановках, не содержащих элементы 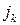 и
и  , совпадают. Больше того, если из перестановок
, совпадают. Больше того, если из перестановок 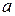 и
и  исключить один из этих элементов, то число инверсий в оставшихся перестановках также будут совпадать, поскольку каждый из них не меняет своего положения относительно других элементов. Тогда становится очевидным, что если
исключить один из этих элементов, то число инверсий в оставшихся перестановках также будут совпадать, поскольку каждый из них не меняет своего положения относительно других элементов. Тогда становится очевидным, что если 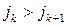 , то
, то  , тогда как в случае
, тогда как в случае  имеем
имеем 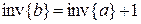 .
.
Следствие 2.3.1. При транспозиции соседних элементов четная перестановка становится нечетной, а нечетная — четной.
Следствие 2.3.2. Любая транспозиция меняет четность перестановки на противоположную.
Теорема 2.3.3. Число четных перестановок всегда совпадает с числом нечетных.
Доказательство. Допустим, что число четных перестановок равно p, а число нечетных q. Если во всех четных перестановках сделать транспозицию (1, 2), то получим p нечетных перестановок, следовательно,  . С другой стороны, если во всех нечетных перестановках также произвести транспозицию (1, 2), то получаем q четных. Но по условию всего их было p, поэтому
. С другой стороны, если во всех нечетных перестановках также произвести транспозицию (1, 2), то получаем q четных. Но по условию всего их было p, поэтому  . Отсюда следует, что
. Отсюда следует, что  .
.
Теорема 2.3.4. Любая перестановка может быть получена из любой другой посредством нескольких транспозиций.
Доказательство. Доказательство проведем методом математической индукции. Если 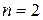 , то утверждение очевидно. Пусть теорема доказана для случая, когда в перестановке
, то утверждение очевидно. Пусть теорема доказана для случая, когда в перестановке  элементов. Докажем утверждение, когда элементов
элементов. Докажем утверждение, когда элементов  .
.
Рассмотрим две произвольные перестановки 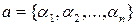 и
и  . Если
. Если 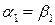 , то поскольку перестановки
, то поскольку перестановки 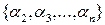 и
и  содержат
содержат  элементов, то в соответствии с индукционным предположением посредством нескольких транспозиций одна из них приводится к другой.
элементов, то в соответствии с индукционным предположением посредством нескольких транспозиций одна из них приводится к другой.
|
|
|
Пусть 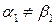 , но, понятно, что существует такой элемент
, но, понятно, что существует такой элемент  , что
, что  . Если сделать транспозицию
. Если сделать транспозицию  в
в  , то получаем перестановку, в которой первый элемент совпадает с первым элементом a. Таким образом, приходим к уже рассмотренному случаю.
, то получаем перестановку, в которой первый элемент совпадает с первым элементом a. Таким образом, приходим к уже рассмотренному случаю.
|
|
|
|
Дата добавления: 2014-01-05; Просмотров: 921; Нарушение авторских прав?; Мы поможем в написании вашей работы!