
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Скалярное произведение векторов
|
|
|
|
Определение 3.16.1. Углом между векторами  и
и 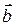 называется наименьший угол между векторами
называется наименьший угол между векторами 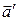 и
и 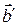 , равными соответственно
, равными соответственно  и
и 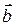 и имеющими общее начало (рис. 3.16.1).
и имеющими общее начало (рис. 3.16.1).
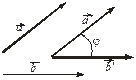
Рис. 3.16.1
Если ненулевые векторы сонаправлены, то угол между ними полагают равным 0, если ненулевые векторы противоположно направлены, то угол между ними считают равным p.
Определение 3.16.2. Скалярным произведением 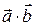 двух векторов
двух векторов  и
и 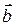 называется произведение их модулей и косинуса угла между
называется произведение их модулей и косинуса угла между  и
и 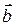 , т. е.
, т. е.
 (3.16.1)
(3.16.1)
Непосредственно из определения следует, что 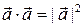 , поэтому
, поэтому  , причем
, причем  , если
, если  .
.
Число 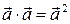 называют скалярным квадратом вектора
называют скалярным квадратом вектора  .
.
Пусть 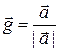 — орт вектора
— орт вектора  , а
, а 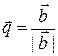 — орт вектора
— орт вектора 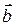 . В соответствии с теоремой 3.11.1 имеем
. В соответствии с теоремой 3.11.1 имеем
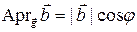 ,
,
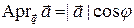 ,
,
поэтому в силу определения скалярного произведения получаем

 . (3.16.2)
. (3.16.2)
Теорема 3.16.1 (свойства скалярного произведения). Для любых трех векторов 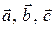 и произвольного числа l справедливы следующие свойства:
и произвольного числа l справедливы следующие свойства:
1. 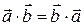 (коммутативность);
(коммутативность);
2. 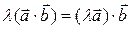 (ассоциативность относительно числового
(ассоциативность относительно числового
множителя);
3. 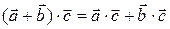 (дистрибутивность относительно суммы
(дистрибутивность относительно суммы
векторов);
4. 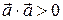 , если
, если  — ненулевой вектор;
— ненулевой вектор;  , если
, если  — нулевой вектор.
— нулевой вектор.
Доказательство. Первое свойство непосредственно вытекает из определения скалярного произведения. Второе и третье свойства справедливы в силу соотношения (3.16.2) и леммы 3.10.1. Действительно, имеем

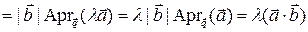 ,
,

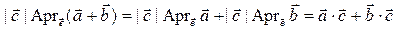 ,
,
где орт 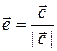 . Наконец, четвертое свойство вытекает непосредственно из определения.
. Наконец, четвертое свойство вытекает непосредственно из определения.
Теорема 3.16.2. Скалярное произведение двух векторов, заданных в произвольной аффинной системе координат  своими координатами
своими координатами  и
и  , находится по формуле
, находится по формуле
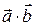 =
= + (α 1 β 2 + α 2 β 1)
+ (α 1 β 2 + α 2 β 1)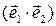 +
+ +
+
+ (α 1 β 3 + α 3 β 1) + (α 2 β 3 + α 3 β 2)
+ (α 2 β 3 + α 3 β 2) +
+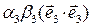 . (3.16.3)
. (3.16.3)
Доказательство. Формула (3.16.3) получается в результате простых вычислений, если воспользоваться представлениями заданных векторов через базис 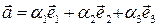 ,
, 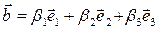 и свойствами скалярного произведения.
и свойствами скалярного произведения.
|
|
|
Величины 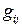 =
=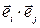 называются метрическими коэффициентами системы координат
называются метрическими коэффициентами системы координат  .
.
Таким образом, для вычисления скалярного произведения двух векторов, заданных своими координатами в аффинной системе координат, необходимо кроме координат этих векторов знать и метрические коэффициенты системы координат.
Следствие 3.16.1. Модуль произвольного вектора  в произвольной аффинной системе координат
в произвольной аффинной системе координат  вычисляется по формуле
вычисляется по формуле
 =
=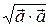 =
=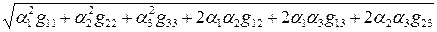 . (3.16.4)
. (3.16.4)
Следствие 3.16.2. Угол j между двумя векторами  и
и 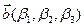 в аффинной системе координат
в аффинной системе координат 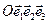 находится по формуле
находится по формуле
j =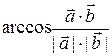 , (3.16.5)
, (3.16.5)
где для вычисления выражения под знаком арккосинуса следует воспользоваться формулами (3.16.3) и (3.16.4).
Следствие 3.16.3. Для векторов, заданных своими координатами в ДПСК, справедливы формулы
n = 3: 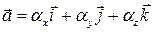 ,
,  ,
,
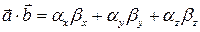 , (3.16.6)
, (3.16.6)
 =
= , (3.16.7)
, (3.16.7)
j =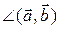 =
= ; (3.16.8)
; (3.16.8)
n = 2:  ,
,  ,
,
 ,
,  =
= ,
,
j =Ð( ) =
) =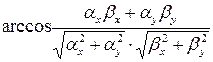 ; (3.16.9)
; (3.16.9)
n = 1: 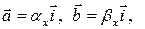

 . (3.16.10)
. (3.16.10)
Поскольку расстояние между двумя точками A (xA, yA, zA) и B (xB, yB, zB) в трехмерном пространстве равно модулю вектора  (x B – x A, y B – y A, z B – z A), то в силу (3.16.7) получаем формулу для нахождения расстояния между названными точками в заданной ДПСК:
(x B – x A, y B – y A, z B – z A), то в силу (3.16.7) получаем формулу для нахождения расстояния между названными точками в заданной ДПСК:
d(A,B) = . (3.16.11)
. (3.16.11)
Аналогично расстояние между двумя точками A (xA, yA) и B (xB, yB) на плоскости находятся по формуле
d(A,B) =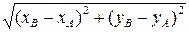 , (3.16.12)
, (3.16.12)
а расстояние между двумя точками A(x A) и B(x B) на прямой соответственно по формуле
d(A,B) = | xB – xA |. (3.16.13)
Теорема 3.16.3. Необходимым и достаточным условием перпендикулярности двух ненулевых векторов в трехмерном пространстве  и
и  , заданных в ДПСК своими координатами, является равенство
, заданных в ДПСК своими координатами, является равенство
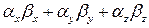 = 0. (3.16.14)
= 0. (3.16.14)
Доказательство непосредственно следует из определения скалярного произведения и выражения (3.16.6).
Теорема 3.16.4. Для декартовых прямоугольных координат вектора  справедливы соотношения
справедливы соотношения
 ,
, 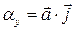 ,
,  . (3.16.15)
. (3.16.15)
Доказательство. Пусть 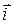 ,
,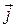 ,
,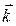 — ортонормированный базис. Вектор
— ортонормированный базис. Вектор 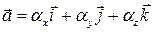 , поэтому
, поэтому
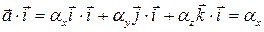 ;
;
 ;
;
 .
.
Рассмотрим в ДПСК  вектор
вектор 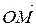 и его орт
и его орт 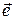 (рис. 3.16.2). Определим углы
(рис. 3.16.2). Определим углы 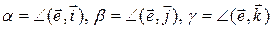 .
.
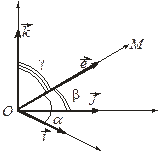
Рис. 3.16.2
|
|
|
Определение 3.16.3. Косинусы cos a, cos b, cos g называются направляющими косинусами вектора 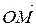 .
.
Теорема 3.16.5. Направляющие косинусы вектора являются декартовыми координатами орта данного вектора.
Доказательство. Пусть 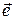 — орт вектора
— орт вектора 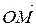 , причем
, причем  . В силу теоремы 3.16.4 и определения скалярного произведения имеем
. В силу теоремы 3.16.4 и определения скалярного произведения имеем
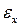 =
= =
=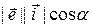 = cos a,
= cos a,
 =
=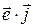 =
=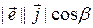 = cos b,
= cos b,
 =
=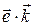 =
=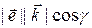 = cos g,
= cos g,
что и требовалось доказать.
Следствие 3.16.4. Для направляющих косинусов справедливо соотношение
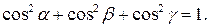
|
|
|
|
Дата добавления: 2014-01-05; Просмотров: 3278; Нарушение авторских прав?; Мы поможем в написании вашей работы!