Способи розв’язування систем лінійних рівнянь

а) Метод Гаусса розв’язування систем лінійних рівнянь

Нехай дано довільну систему m лінійних рівнянь з п невідомими

У даній системі хоча б один із коефіцієнтів біля невідомої х₁ відмінний від нуля, бо інакше система не мала б п невідомих. Якщо а₁₁=0, але а_s1 ≠ 0, то переставивши перше та s -те рівняння, отримаємо еквівалентну систему, у першому рівнянні якої коефіцієнт при х₁ буде відмінним від нуля. Тому вважатимемо, що а₁₁ ≠ 0.

Запишемо розширену матрицю системи, відокремивши стовпчик вільних членів:

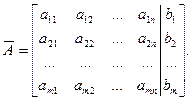
Застосовуючи елементарні перетворення рядків, зведемо дану матрицю до ступінчастого вигляду. Систему лінійних рівнянь, розширена матриця якої ступінчаста, також називають ступінчастою. Ясно, що ступінчаста система еквівалентна початковій системі. Перетворення системи лінійних рівнянь у ступінчасту систему називають зведенням системи лінійних рівнянь до ступінчастого вигляду. Позначимо ступінчасту матрицю, отриману з матриці 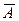, через .

Розглянемо такі можливі випадки:

1. У розширеній матриці є рядок, в якому першим ненульовим елементом є його останній елемент.

2. У матриці такого рядка немає.

В першому випадку в ступінчастій системі міститься рівняння вигляду де b ≠ 0. Оскільки жодна система чисел 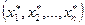не може задовольнити рівняння 0=b, де b ≠ 0, то така ступінчаста система несу-місна.

В другому випадку ступінчаста система містить r ненульових рядків і нехай перші ненульові елементи цих рядків знаходяться в стовпчиках з номерами k₁=1, k₂, k₃, …, k_r, де k₁ <k₂ <k₃ <…< k_r < n. Всі рівняння системи вигляду 0·х₁+0·х₂+…+0·х_n=0 відкинемо. Невідомі , з яких починається перше, друге,…, r -те рівняння системи, називають головними, а всі інші (якщо вони є) – вільними.

Якщо вільних невідомих немає, тоді r=n, звідки k₁=1, k₂=2, k₃=3, …, k_r=n, і система матиме трикутний вигляд:

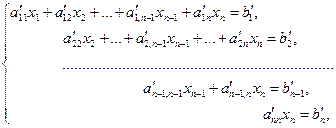
де

Із останнього рівняння знаходимо х_п, а потім, підставивши його в попереднє рівняння, знаходимо х_п-1, і т.д., в результаті отримаємо єдині значення невідомих, які і становлять єдиний розв’язок 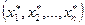системи. Отже, при відсутності вільних невідомих ступінчаста система лінійних рівнянь сумісна і визначена.

Якщо вільні невідомі є, то система має вигляд:

де 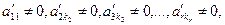1<k₂<k₃<…<k_r<n.

Позначимо символом В_і суму всіх тих членів і -го рівняння системи, які містять вільні невідомі. Перенесемо члени з вільними невідомими в праві частини рівнянь і отримаємо:

де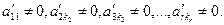

Надавши вільним невідомим довільно вибраних числових значень, отримаємо попередній випадок системи без вільних невідомих, який дає єдині значення головних невідомих 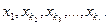Сукупність знайдених значень головних невідомих і вибраних нами значень вільних невідомих, ясно, є цілком визначеним розв’язком ступінчастої системи, який відповідає вибраним значенням вільних невідомих. Оскільки значення вільних невідомих можна вибрати довільно, то множина різних наборів, а, значить, множина розв’язків ступінчастої системи є нескінченною. Таким чином, при наявності вільних невідомих ступінчаста система лінійних рівнянь сумісна, але невизначена.

Іншими словами, доведено теореми:

Теорема 1. Система лінійних рівнянь сумісна тоді і тільки тоді, коли вона зводиться до ступінчастої системи, в якій немає рівнянь вигляду 0=b, де b≠0.

Теорема 2. Система лінійних рівнянь є визначеною тоді і тільки тоді, коли вона зводиться до ступінчастої системи, в якій число рівнянь r дорівнює числу невідомих n.

Наслідок 1. Система лінійних рівнянь з п невідомими є визначеною тоді і тільки тоді, коли вона зводиться до ступінчастої системи, в якій

Наслідок 2. Сумісна система m лінійних рівнянь з п невідомими при m<n є невизначеною.

Дата добавления: 2014-01-05