
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Преобразование Лапласа. Понятие передаточной функции. Преобразование Лапласа связывает функцию F(s) (изображение) комплексной переменной s с соответствующей функцией f(t) (оригиналом) действительной переменной t
|
|
|
|
Преобразование Лапласа связывает функцию F(s) (изображение) комплексной переменной s с соответствующей функцией f(t) (оригиналом) действительной переменной t. Это соответствие, по существу, взаимно однозначное для большинства практических целей. Преобразование Лапласа характерно тем, что многим соотношениям и операциям над оригиналами f(t) соответствуют более простые соотношения и операции над их изображениями F(s). Оно применяется, в частности, для решения дифференциальных и интегральных уравнений. Подход заключается в преобразовании уравнения, содержащего оригиналы f(t), в эквивалентное уравнение относительно соответствующих изображений Лапласа F(s), где s = s + j w.
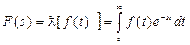
|
Рассмотрим основные свойства преобразований Лапласа:
- дифференцирование оригинала
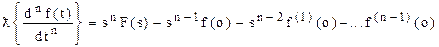
|
- интегрирование оригинала
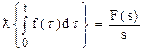
|
- линейность
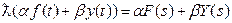
|
- изменение масштаба
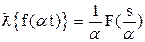
|
- сдвиг аргумента у оригинала
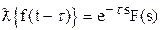
|
Пусть динамика системы управления описывается уравнением вида:
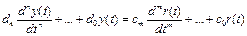
|
где y(t) - управляемый параметр, r(t) - внешнее воздействие, вызывающее реакцию системы управления. Предполагаем, что имеют место нулевые начальные условия, то есть до приложения внешнего воздействия система находится в состоянии равновесия (в установившемся состоянии). Применим к обеим частям уравнения динамики преобразование Лапласа, получим:
(d sn +...+ d sn +...+ d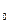 ) Y (s) = (cm sm +... +co) R (s) ) Y (s) = (cm sm +... +co) R (s)
|
Проследим связь входных и выходных величин:
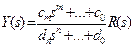
|
Введем функцию вида
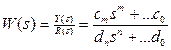
| (1.6) |
эта функция является передаточной. Определение ее следующее: передаточной функцией называется отношение преобразования Лапласа выходной величины к входной при нулевых начальных условиях.
|
|
|
Передаточная функция элементов и систем является одной из важнейших характеристик, определяющей динамические свойства. Отметим, что для всех реальных объектов степень полинома числителя передаточной функции небольше степени полинома знаменателя. Обратный переход от изображения к оригиналу может осуществляться на основе обратного преобразования Лапласа, если оно существует. В частности, для каждого t > 0, где f(t) является функцией непрерывной, справедлива формула
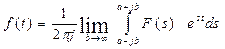
|
где a - абсцисса абсолютной сходимости, то есть такая величина, при которой выполняется условие:
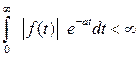
|
Для рациональных алгебраических функций обычно применяется разложение Хевисайда, рассмотрим его. Если учесть, что
| C(s) = cm sm +...+ c0, D(s) = dn sn +...+ d0 |
представляют собой полином числителя и полином знаменателя функции W (s), и если корни полинома знаменателя не кратные, то оригинал можно представить в виде:
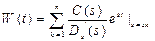 ; ; 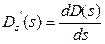 (t >0); (t >0);
|
Перейдем к рассмотрению типовых звеньев систем регулирования, то есть их математических моделей в виде простых передаточных функций.
|
|
|
|
Дата добавления: 2014-01-05; Просмотров: 360; Нарушение авторских прав?; Мы поможем в написании вашей работы!