Определение касательных напряжений

В общем случае изгиба в поперечных сечениях балки возникают изгибающие моменты и поперечные силы. Наличие изгибающего момента связано с возникновением в поперечных сечениях балки нормальных напряжений, для определения которых можно пользоваться формулой (6.3).

Наличие поперечной силы обуславливает возникновение касательных напряжений в сечениях балки, а по закону парности касательных напряжений, и в ее продольных сечениях, рис. 6.14.

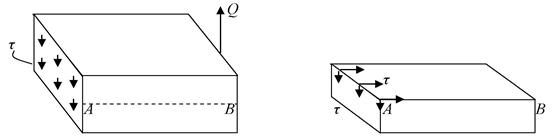
(а) (б)

Рис. 6.14

Закон распределения τ по высоте балки не известен.

Для расчета касательных напряжений выделим элемент dz по длине балки, рис. 6.15, а

(а) (б) (в)

Рис. 6.15

Проведем горизонтальное сечение на расстоянии y от нейтральной линии и рассмотрим равновесие отсеченной части с основанием b, рис. 6.15, в, г. По закону парности сдвиговые напряжения в продольных сечениях равны сдвиговым напряжениям в поперечных сечениях.

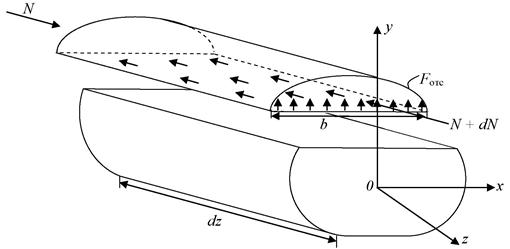
(г)

Рис. 6.15

Рассмотрим условие равновесия отсеченной части

.

Последнее слагаемое есть сила, собираемая с площади продольного сечения bdz и обусловленная действием равномерно-распределенных по этой площади касательных напряжений τ. Из последнего уравнения выражаем τ

. (6.4)

С другой стороны, нормальная сила N есть равнодействующая нормальных напряжений, действующих по отсеченной площади поперечного сечения F _отс параллельно 0 z

.

При этом сами нормальные напряжения выразятся как

,

где 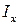, как и прежде, момент инерции поперечного сечения относительно оси x. Объединяя две последние формулы, получим

.

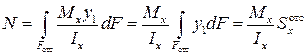Здесь 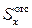- статический момент отсеченной площади относительно оси x. Дифференцируя последнее выражение, находим

.

Подставим последнее выражение в (6.4)

.

Вспоминая, что производная момента по координате z согласно теореме Журавского есть поперечная сила Q_z, получим окончательное выражение для сдвиговых напряжений

. (6.5)

Согласно (6.5), касательное напряжение может быть рассчитано для любого поперечного сечения балки, в котором известна поперечная сила Q_z. При этом сила Q_z и момент инерции I_x постоянны для каждого сечения. Переменными по координате y (отсчитываемой от нейтрального сечения по высоте балки) являются только 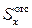и b.

В качестве примера рассмотрим расчет τ для балки прямоугольного сечения, рис. 6.16.

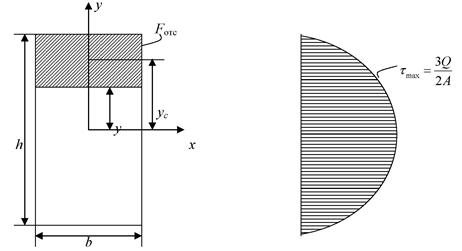
(a) (б)

Рис. 6.16

В данном примере по высоте сечения балки будут постоянны не только Q_z и I_x, но и ширина отсеченной части b. Статический момент отсеченной площади можно рассчитать как

,

,

.

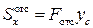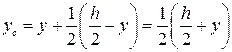Подставляя выражения и в выражение для , находим

.

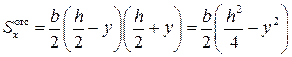Рассчитаем τ по (6.5)

. (6.6)

Максимальное значение τ будет при y = 0 на нейтральном слое

,

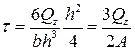где A = bh. При этом согласно (6.6) касательные напряжения равны нулю на поверхности балки. Эпюра касательных напряжений приведена на рис. 6,16.

Дата добавления: 2014-01-05